
【题目】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2﹣ab﹣bc﹣ac= ![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美;
[(a﹣b)2+(b﹣c)2+(a﹣c)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美;
(1)请你检验说明这个等式的正确性.
(2)若a=2011,b=2012,c=2013,你能很快求出a2+b2+c2﹣ab﹣bc﹣ac的值吗?
(3)若a﹣b= ![]() ,b﹣c=
,b﹣c= ![]() ,a2+b2+c2=1,求ab+bc+ac的值.
,a2+b2+c2=1,求ab+bc+ac的值.
【答案】
(1)解:等式右边= ![]() (a2﹣2ab+b2+b2﹣2bc+c2+a2﹣2ac+c2)=
(a2﹣2ab+b2+b2﹣2bc+c2+a2﹣2ac+c2)= ![]() (2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)=a2+b2+c2﹣ab﹣bc﹣ac=左边,得证
(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)=a2+b2+c2﹣ab﹣bc﹣ac=左边,得证
(2)解:当a=2011,b=2012,c=2013时,a2+b2+c2﹣ab﹣bc﹣ac= ![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2]=3
[(a﹣b)2+(b﹣c)2+(a﹣c)2]=3
(3)解:∵a﹣b= ![]() ,b﹣c=
,b﹣c= ![]() ,∴a﹣c=
,∴a﹣c= ![]() ,
,
∵a2+b2+c2=1,
∴ab+bc+ac=a2+b2+c2﹣ ![]() [(a﹣b)2+(b﹣c)2+(a﹣c)2]=1﹣
[(a﹣b)2+(b﹣c)2+(a﹣c)2]=1﹣ ![]() (
( ![]() +
+ ![]() +
+ ![]() )=﹣
)=﹣ ![]()
【解析】(1)等式右边中括号中利用完全平方公式站那看,合并后去括号得到结果,与左边比较即可得证;(2)根据(1)中的结论,将a,b,c的值代入右边计算即可求出值;(3)由题意求出a﹣c的值,所求式子利用完全平方公式变形,将各自的值代入计算即可求出值.
【考点精析】本题主要考查了因式分解的应用的相关知识点,需要掌握因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程才能正确解答此题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】(1)如图,在⊙O中,AC∥OB,∠BAO=25°,求∠BOC的度数.
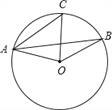
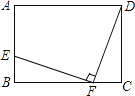
(2)已知:如图,在矩形ABCD中,点E在边AB上,点F在边BC上,且BE=CF,EF⊥DF,求证:BF=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某产品原来每件成本128元,经过连续两年技术改造与强化管理,每件成本降为98元,假设成本每年下降的百分数相同.设每年的平均下降率为x,则可列方程为( )
A. 128(1﹣x)2 = 98B. 128(1+x)2= 98
C. 98(1﹣x)2 = 128D. 98(1+x)2 = 128
查看答案和解析>>
科目:初中数学 来源: 题型:
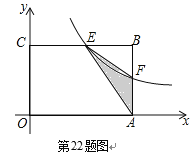
【题目】(本题满分8分)
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数![]() 的图象与BC边交于点E.
的图象与BC边交于点E.
⑴当F为AB的中点时,求该函数的解析式;
⑵当k为何值时,△EFA的面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使多项式(x2+px+2)(x﹣q)不含关于x的二次项,则p与q的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 乘积为﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
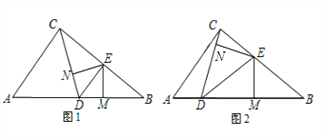
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D在边AB上运动,DE平分∠CDB交边BC于点E,EM⊥BD垂足为M,EN⊥CD垂足为N.
(1)当AD=CD时,求证:DE∥AC;
(2)探究:AD为何值时,△BME与△CNE相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com