
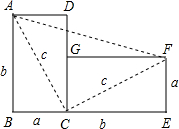
 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
(
|
| 5 |
| 4 |
| 5 |
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
(
|
| 6 |
| 5 |
| 1 | ||||
|
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、函数y=2(x-1)2-1的一次项系数是-4 |
| B、“明天降雨的概率是50%”表示明天有半天都在降雨 |
| C、若a为实数,则|a|<0是不可能事件 |
| D、一个盒子中有白球m个,红球6个,黑球n个(每个球除了颜色外都相同),如果从中任取一个球,取得的是红球的概率与不是红球的概率相同,那么m与n的和是6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 12 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com