
| 12 |
| 2 |
| 1 |
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
| 3 |
|
|


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
 抛物线y=x2-4x+3
抛物线y=x2-4x+3查看答案和解析>>
科目:初中数学 来源: 题型:
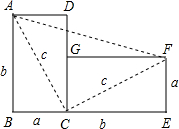 如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.查看答案和解析>>
科目:初中数学 来源: 题型:
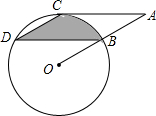 如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.
如图,点B、C、D都在⊙O上,过点C的⊙O的切线交OB延长线于点A,C连接CD、BD,若∠CDB=∠OBD=30°,OB=6cm.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com