
【题目】如图,已知平行四边形ABCD的两条对角线相交于点O,E是BO的中点,过B点作AC的平行线,交CE的延长线于点F,连接BF。
(1)求证:FB=AO;
(2)平行四边形ABCD满足什么条件时,四边形AFBO是矩形?说明理由.

【答案】(1)证明见解析;(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.
【解析】
(1)证明△BEF≌△OEC,即可得出结论;
(2)先证明四边形AFBO是平行四边形,然后根据OA⊥OB得到平行四边形AFBO是矩形.
证明:(1)∵E是BO的中点,
∴OE=BE,
∵BF∥AC,
∴∠BFE=∠OCE,
在△BEF和△OEC中,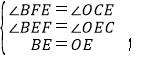
∴△BEF≌△OEC,
∴BF=OC,
∵平行四边形ABCD的两条对角线相交于点O,
∴OA=OC,
∴FB=AO;
(2)当平行四边形ABCD是菱形时,四边形AFBO是矩形.理由如下:
∵BF∥AC,FB=AO,
∴四边形AFBO是平行四边形,
∵平行四边形ABCD是菱形,
∴OA⊥OB,
∴∠AOB=90°.
∴平行四边形AFBO是矩形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作![]() ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.

(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠ACD=30°,BD=6,
求(1)∠BAD,∠ABC的度数;
(2)求AB,AC的长;
(3)求菱形ABCD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.
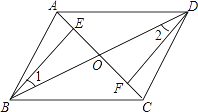
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A 角翻折,使得点A落在EF上的点A′处,折痕交AE于点G,则EG=_________cm.
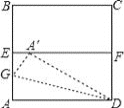
查看答案和解析>>
科目:初中数学 来源: 题型:
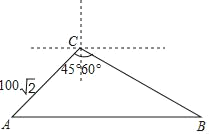
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒.
(1)请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数).
≈1.73,计算结果保留两位小数).
(2)请你以交通警察叔叔的身份对此小轿车的行为作出处理意见,并就乡村公路安全管理提出自己的建议。(处理意见合情合理,建议尽量全面。)
查看答案和解析>>
科目:初中数学 来源: 题型:
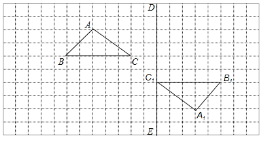
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(三角形顶点是网格线的交点)和△A1B1C1,且△ABC与△A1B1C1,成中心对称.
(1)画出△ABC和△A1B1C1的对称中心![]() ;
;
(2)将△A1B1C1沿直线![]() 方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
方向向上平移6格,得到△A2B2C2,画出△A2B2C2;
(3)将△A2B2C2绕点C2顺时针方向旋转90°,得到△A3B3C3,画出△A3B3C3.
查看答案和解析>>
科目:初中数学 来源: 题型:
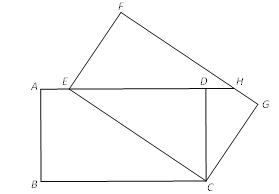
【题目】如图,将矩形ABCD绕点C旋转得到矩形FECG,点E在AD上,延长ED交FG于点H.
(1)求证:△EDC≌△HFE;
(2)连接BE、CH.
①四边形BEHC是怎样的特殊四边形?证明你的结论.
②当AB与BC的比值为 时,四边形BEHC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有三个点![]() ,
,![]() 是
是![]() 的边
的边![]() 上一点,
上一点,![]() 经平移后得到
经平移后得到![]() ,点
,点![]() 的对应点为
的对应点为![]() .
.
(1)画出平移后的![]() ,写出点
,写出点![]() 的坐标;
的坐标;
(2)![]() 的面积为_________________;
的面积为_________________;
(3)若点![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的关系式(用含
之间的关系式(用含![]() 的式子表示
的式子表示![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com