
【题目】如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=18,OC=12,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点B的坐标是 ;
(2)求直线DE的函数表达式;
(3)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,求当S△PDE=2S△OCD时t的值.

【答案】(1)(18,12);(2)y=![]() x﹣
x﹣![]() ;(3)当S△PDE=2S△OCD时,t的值为10,
;(3)当S△PDE=2S△OCD时,t的值为10,![]() ,40
,40
【解析】
(1)根据矩形的性质可得AB=OC=12,BC=AO=18,可求点B坐标;
(2)由折叠的性质可得AD=CD,∠ADE=∠CDE,根据勾股定理可求OD=5,即CD=AD=13,根据等腰三角形的性质可求CE=13,即可得点D,点E的坐标,则用待定系数法可求直线DE的函数表达式;
(3)分点P在AD上,AB上,BC上三种情况讨论,根据三角形面积的求法可求t的值.
(1)∵四边形ABCO是矩形,
∴AB=OC,BC=AO,
∵OA=18,OC=12,
∴AB=12,BC=18,
∴点B坐标(18,12)
故答案为:(18,12)
(2)∵折叠
∴AD=CD,∠ADE=∠CDE,
∵OC2+OD2=CD2,
∴144+OD2=(18﹣OD)2,
∴OD=5,
∴CD=13,点D坐标为(5,0),
∵BC∥AO,
∴∠CED=∠EDA,且∠ADE=∠CDE,
∴∠CED=∠CDE,
∴CE=CD=13,
∴点E坐标为(13,12),
设直线DE的函数表达式为y=kx+b,
∴![]()
解得:k=![]() ,b=﹣
,b=﹣![]()
∴解析式y=![]() x﹣
x﹣![]()
(3)∵S△PDE=2S△OCD,
∴S△PDE=2×![]() ×OC×OD=12×5=60
×OC×OD=12×5=60
当点P在AD上时,S△PDE=![]() ×PD×12=60,
×PD×12=60,
∴PD=10
∴t=![]() =10,
=10,
当点P在AB上时,S△PDE=S梯形ABED﹣S△PBE﹣S△APD=108﹣![]() ×5×(12﹣AP)﹣
×5×(12﹣AP)﹣![]() ×13×AP=60
×13×AP=60
∴AP=![]()
∴t=![]() =
=![]()
当点P在BC上时,S△PDE=![]() ×PE×12=60
×PE×12=60
∴PE=10
∴t=![]() =40
=40
综上所述:当S△PDE=2S△OCD时,t的值为10,![]() ,40.
,40.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程(组)解应用题:2019年11月2日-4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.你认为这个规则公平吗?请用列表法或画树状图法加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读如下材料,然后解答后面的问题:已知直线l1:y=﹣2x﹣2和直线l2:y=﹣2x+4如图所示,可以看到直线l1∥l2,且直线l2可以由直线l1向上平移6个长度单位得到,直线l2可以由直线l1向右平移3个长度单位得到.这样,求直线l2的函数表达式,可以由直线l1的函数表达式直接得到.即:如果将直线l1向上平移6的长度单位后得到l2,得l2的函数表达式为:y=﹣2x﹣2+6,即y=﹣2x+4;如果将直线l1向右平移3的长度单位后得到得l2,l2的函数表达式为:y=﹣2(x﹣3)﹣2,即y=﹣2x+4.
(1)将直线y=2x﹣3向上平移2个长度单位后所得的直线的函数表达式是 ;
(2)将直线y=3x+1向右平移m(m>0)两个长度单位后所得的直线的函数表达式是 ;
(3)已知将直线y=![]() x+1向左平移n(n>0)个长度单位后得到直线y=
x+1向左平移n(n>0)个长度单位后得到直线y=![]() x+5,则n= .
x+5,则n= .
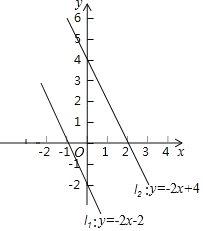
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完成这批零件,甲车间工作了8个小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止.设甲、乙两车间各自加工零件的数量为![]() (个),甲车间加工的时间为
(个),甲车间加工的时间为![]() (时),
(时),![]() 与
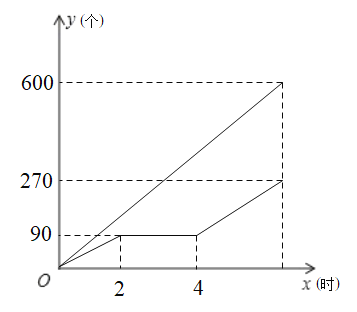
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲车间每小时加工零件的个数为_________个;这批零件的总个数为__________个;
(2)求乙车间维护设备后,乙车间加工零件的数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在加工这批零件的过程中,当甲、乙两车间共同加工完成810个零件时,求甲车间加工的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习题:问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上.
思维拓展:(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
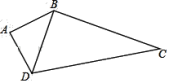
【题目】如图,在四边形ABCD中,AB=4,AD=3,AB⊥AD ,BC=12.
(1)求BD的长;
(2)当CD为何值时,△BDC是以CD为斜边的直角三角形?
(3)在(2)的条件下,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com