
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完成这批零件,甲车间工作了8个小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止.设甲、乙两车间各自加工零件的数量为![]() (个),甲车间加工的时间为
(个),甲车间加工的时间为![]() (时),
(时),![]() 与
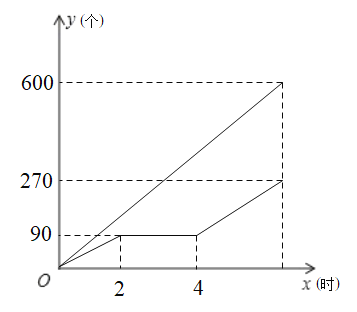
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲车间每小时加工零件的个数为_________个;这批零件的总个数为__________个;
(2)求乙车间维护设备后,乙车间加工零件的数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在加工这批零件的过程中,当甲、乙两车间共同加工完成810个零件时,求甲车间加工的时间.
【答案】(1)75,870;(2)![]() ;(3)甲车间加工的时间为7.5个小时.
;(3)甲车间加工的时间为7.5个小时.
【解析】
(1)根据图像可知甲8个小时加工了600个零件,乙8个小时加工了270个零件,据此填空即可;
(2)设![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,由图像知该函数过点
,由图像知该函数过点![]() ,利用待定系数法求解即可;
,利用待定系数法求解即可;
(3)设甲车间加工了x个小时,根据甲乙总共加工810个零件列方程求解即可.
解:(1)由图像得甲8个小时加工了600个零件,![]() (个),
(个),
![]() (个),
(个),
所以甲车间每小时加工零件的个数为75个;这批零件的总个数为870个;
(2)设![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ,由图像知该函数过点
,由图像知该函数过点![]() ,
,
将点![]() 代入得
代入得![]()
解得![]()
所以![]() 与
与![]() 之间的函数关系式为
之间的函数关系式为![]() ;
;
(3)由图像得乙的设备维修了2个小时,乙每小时加工![]() 个
个
设甲车间加工了x个小时,则乙车间加工了![]() 个小时
个小时
根据题意得![]()
解得![]()
所以甲车间加工的时间为7.5个小时.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】两个反比例函数![]() 和
和![]() 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在![]() 的图象上,PC⊥
的图象上,PC⊥![]() 轴于点C,交
轴于点C,交![]() 的图象于点A,PC⊥
的图象于点A,PC⊥![]() 轴于点D,交
轴于点D,交![]() 的图象于点B. 当点P在
的图象于点B. 当点P在![]() 的图象上运动时,以下结论:
的图象上运动时,以下结论:
①![]()
②![]() 的值不会发生变化
的值不会发生变化
③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
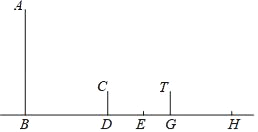
【题目】如图,花丛中有一路灯AB,在灯光下,小明在D点处的影长DE=3m,沿BD方向走到G点,DG=5m,这时,小明的影长GH=5m,小明的身高为1.7m.
(1)画出路灯灯泡A的位置.
(2)求AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知长方形OABC的顶点A在x轴上,顶点C在y轴上,OA=18,OC=12,D、E分别为OA、BC上的两点,将长方形OABC沿直线DE折叠后,点A刚好与点C重合,点B落在点F处,再将其打开、展平.
(1)点B的坐标是 ;
(2)求直线DE的函数表达式;
(3)设动点P从点D出发,以1个单位长度/秒的速度沿折线D→A→B→C向终点C运动,运动时间为t秒,求当S△PDE=2S△OCD时t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举办“校园好声音”朗诵大赛,根据初赛成绩,七年级和八年级各选出5名选手组成七年级代表队和八年级代表队参加学校决赛两个队各选出的5名选手的决赛成绩如图所示:
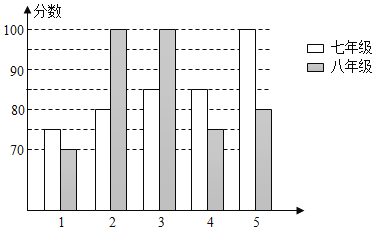
(1)根据所给信息填写表格;
平均数(分) | 中位数(分) | 众数(分) | |
七年级 | 85 | ||
八年级 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)若七年级代表队决赛成绩的方差为70,计算八年级代表队决赛成绩的方差,并判断哪个代表队的选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
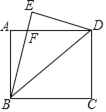
【题目】如图,将矩形ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
(1)求证:△ABF≌△EDF;
(2)若AB=6,BC=8,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为(a,0)和(c,0).则这两个点所成的线段的长为|a﹣c|;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b﹣d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a﹣c|,P2Q=|b﹣d|,利用勾股定理可得:线段P1P2的长为![]() .
.
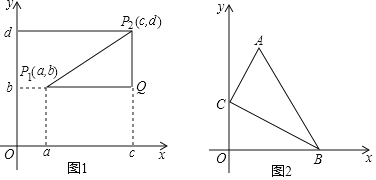
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知A(6,﹣1),B(6,5),则线段AB的长为 ;
(2)若点C在y轴上,点D的坐标是(﹣3,0),且CD=6,则点C的坐标是 ;
(3)如图2,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com