
【题目】如图,已知P、Q分别是⊙O的内接正六边形ABCDEF的边AB、BC上的点,AP=BQ,则∠POQ的度数为___°.

【答案】60
【解析】
连接OA、OB、OC,证明△OBP≌△OCQ,根据全等三角形的性质得到∠BOP=∠COQ,结合图形计算即可.
连接OA、OB、OC,
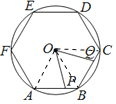
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠AOB=∠BOC=60°,
∵OA=OB,OB=OC,
∴∠OBA=∠OCB=60°,
∵AP=BQ,AB=BC,
∴BP=CQ,
在△OBP和△OCQ中,
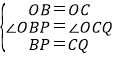 ,
,
∴△OBP≌△OCQ,
∴∠BOP=∠COQ,
∵∠AOB=∠AOP+∠BOP,∠BOC=∠BOQ+∠QOC,
∴∠BOP=∠QOC,
∵∠POQ=∠BOP+∠BOQ,∠BOC=∠BOQ+∠QOC,
∴∠POQ=∠BOC=60°.
故答案为:60°.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,联结BD,给出下列条件:∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABD∽△ACB的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车间同时开始加工一批零件,从开始加工到加工完成这批零件,甲车间工作了8个小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批零件的加工任务为止.设甲、乙两车间各自加工零件的数量为![]() (个),甲车间加工的时间为
(个),甲车间加工的时间为![]() (时),
(时),![]() 与
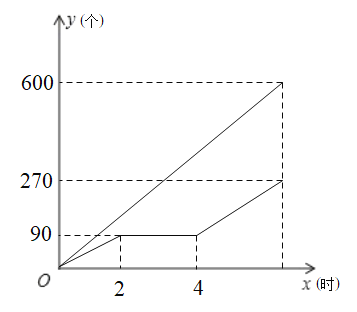
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
(1)甲车间每小时加工零件的个数为_________个;这批零件的总个数为__________个;
(2)求乙车间维护设备后,乙车间加工零件的数量![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在加工这批零件的过程中,当甲、乙两车间共同加工完成810个零件时,求甲车间加工的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
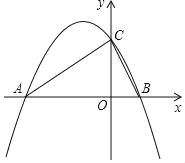
【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣4,0),B (1,0)两点,与y轴交于点C.
(1)求这个二次函数的解析式;
(2)连接AC、BC,判断△ABC的形状,并证明;
(3)若点P为二次函数对称轴上点,求出使△PBC周长最小时,点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现场学习题:问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.

(1)请你将△ABC的面积直接填写在横线上.
思维拓展:(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为![]() 、
、![]() 、
、![]() (a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
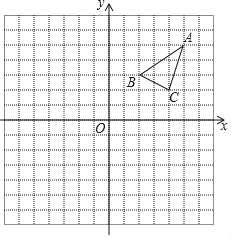
【题目】已知△ABC在平面直角坐标系中的位置如图所示,
(1)先画出△ABC关于x轴对称的图形△A1B1C1,再画出△A1B1C1关于y轴对称的图形△A2B2C2;
(2)直接写出△A2B2C2各顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
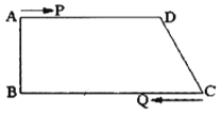
【题目】如图,在四边形ABCD中,AD//BC,![]() ,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
(1)当运动时间为t秒时,用含t的代数式表示以下线段的长: AP=________, BQ=__________;
(2)当运动时间为多少秒时,四边形PQCD为平行四边形?
(3)当运动时间为多少秒时,四边形ABQP为矩形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com