
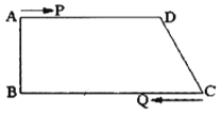
【题目】如图,在四边形ABCD中,AD//BC,![]() ,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
,AD=24 cm,AB=8 cm, BC=26 cm,动点P从A开始沿AD边向D以1cm/s的速度运动;Q从点C开始沿CB边向B以3 cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动.
(1)当运动时间为t秒时,用含t的代数式表示以下线段的长: AP=________, BQ=__________;
(2)当运动时间为多少秒时,四边形PQCD为平行四边形?
(3)当运动时间为多少秒时,四边形ABQP为矩形?
【答案】(1)t,26-3t;(2)运动时间为6秒时,四边形PQCD为平行四边形.(3)运动时间为![]() 秒时,四边形ABQP为矩形.
秒时,四边形ABQP为矩形.
【解析】
(1)根据题意可直接得出;
(2)由在梯形ABCD中,AD∥BC,可得当PD=CQ时,四边形PQCD是平行四边形,即可得方程:24-t=3t,解此方程即可求得答案;
(3)由在梯形ABCD中,AD∥BC,∠B=90°,可得当AP=BQ时,四边形ABQP是矩形,即可得方程:t=26-3t,解此方程即可求得答案.
解:(1)由题意知AP=t,BQ=26-3t,
故答案为:t,26-3t;
(2)由题意可得:PD=AD-AP=24-t,QC=3t,
∵AD∥BC,
∴PD∥QC,
设当运动时间为t秒时PD=QC,此时四边形PQCD为平行四边形.
由PD=QC得,24-t=3t,
解得:t=6,
∴当运动时间为6秒时,四边形PQCD为平行四边形.
(3)∵AD∥BC,
∴AP∥BQ,
设当运动时间为t秒时AP=BQ,四边形ABQP为平行四边形.
由AP=BQ得:t=26-3t,
解得:t=![]() ,
,
又∵∠B=90°
∴平行四边形ABQP为矩形.
∴当运动时间为![]() 秒时,四边形ABQP为矩形.
秒时,四边形ABQP为矩形.


科目:初中数学 来源: 题型:
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为(a,0)和(c,0).则这两个点所成的线段的长为|a﹣c|;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b﹣d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a﹣c|,P2Q=|b﹣d|,利用勾股定理可得:线段P1P2的长为![]() .
.
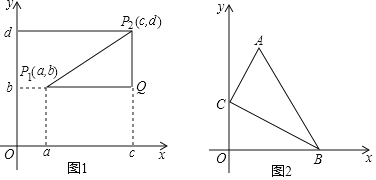
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知A(6,﹣1),B(6,5),则线段AB的长为 ;
(2)若点C在y轴上,点D的坐标是(﹣3,0),且CD=6,则点C的坐标是 ;
(3)如图2,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
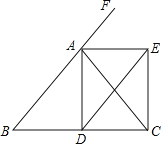
【题目】如图,已知△ABC中,AB=AC,AD是角平分线,F为BA延长线上的一点,AE平分∠FAC,DE∥BA交AE于E.求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的△ABC中,AB>AC>BC,且D为BC上一点。现打算在AB上找一点P,在AC上找一点Q,使得△APQ与以P、D、Q为顶点的三角形全等,以下是甲、乙两人的作法:
甲:连接AD,作AD的中垂线分别交AB、AC于P点、Q点,则P、Q两点即为所求;
乙:过D作与AC平行的直线交AB于P点,过D作与AB平行的直线交AC于Q点,则P、Q两点即为所求;
对于甲、乙两人的作法,下列判断何者正确( )?

A.两人皆正确B.两人皆错误C.甲正确,乙错误D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() .
.
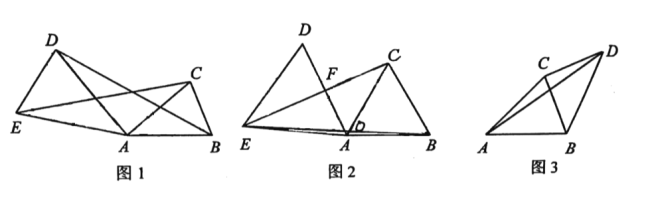
(1)如图1,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图3,在![]() 中,
中,![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com