
����Ŀ���Ȱ�ѧϰ��С��ͬѧ��������������������ֲ��ϣ�
��x���������������ǵ�����ֱ�Ϊ��a��0���ͣ�c��0�����������������ɵ��߶εij�Ϊ|a��c|��ͬ��������y���ϵ���������ֱ�Ϊ��0��b���ͣ�0��d�����������������ɵ��߶εij�Ϊ|b��d|����ͼ1����ֱ������ϵ�е���������P1��P2��������ֱ�Ϊ��a��b���ͣ�c��d�����ֱ���������������������ƽ���ߣ�����һ��ֱ�������Σ�����ֱ�DZ�P1Q=|a��c|��P2Q=|b��d|�����ù��ɶ����ɵã��߶�P1P2�ij�Ϊ![]() ��
��
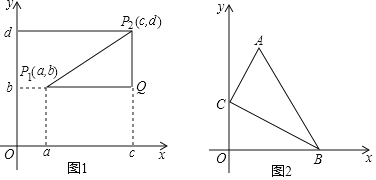
����������ϣ��ش���������⣺
��1����ƽ��ֱ������ϵ�У���֪A��6����1����B��6��5�������߶�AB�ij�Ϊ ��
��2������C��y���ϣ���D�������ǣ���3��0������CD=6�����C�������� ��
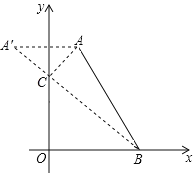
��3����ͼ2����ֱ������ϵ�У���A��B������ֱ�Ϊ��1��4���ͣ�3��0������C��y���ϵ�һ�����㣬��A��B��C���㲻��ͬһ��ֱ���ϣ����ABC�ܳ�����Сֵ��
���𰸡���1��6����2��![]() ��
��![]() ����3��
����3��![]() ��
��
��������
��1�������߶γ��ȼ��㷽�����㼴�ɣ�
��2����C������Ϊ��0��b���������߶γ��ȼ��㷽�����㼴�ɣ�
��3���ҵ���A����y��ĶԳƵ�A'����1��4��������A'B��y���ڵ�C����ʱ��ABC�ܳ�����С��Ȼ������߶γ��ȼ��㷽��������⣮
�⣺��1����A��6����1����B��6��5����
��![]() ��
��
�ʴ�Ϊ��6��
��2����C��������0��b����
����Rt��OCD��CD2=OC2+OD2��������3��0��2+��0��b��2=62��
���![]() ��
��
����C������Ϊ![]() ��
��![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3����ͼ����A�����y��ĶԳƵ�ΪA'�����A'������Ϊ����1��4����A'C = AC��
�ߡ�ABC���ܳ�=AB+ AC+CB=AB+ A'C+CB�������߶�AB�ij�Ϊ��ֵ��
�൱C��ΪA'B��y��Ľ���ʱ����ʱA'B��ΪA'C+CB����Сֵ����ABC���ܳ���С��
��ʱ��ABC���ܳ�=AB+A'C+CB= AB+A'B��
�ߵ�A��B������ֱ�Ϊ��1��4���ͣ�3��0����
��AB![]() 2
2![]() ��
��![]() ��
��
���ԡ�ABC���ܳ�����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
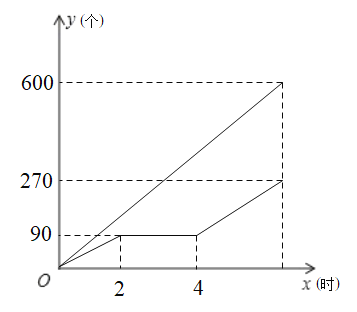
����Ŀ���ס���������ͬʱ��ʼ�ӹ�һ��������ӿ�ʼ�ӹ����ӹ��������������׳��乤����8��Сʱ���ҳ�������;ͣ��һ��ʱ��ά���豸��Ȼ��ͣ��ǰ�Ĺ���Ч�ʼ����ӹ���ֱ����׳���ͬʱ�����������ļӹ�����Ϊֹ.��ס�����������Լӹ����������Ϊ![]() ���������׳���ӹ���ʱ��Ϊ
���������׳���ӹ���ʱ��Ϊ![]() ��ʱ����
��ʱ����![]() ��
��![]() ֮��ĺ���ͼ����ͼ��ʾ.
֮��ĺ���ͼ����ͼ��ʾ.
��1���׳���ÿСʱ�ӹ�����ĸ���Ϊ_________��������������ܸ���Ϊ__________����
��2�����ҳ���ά���豸���ҳ���ӹ����������![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3���ڼӹ���������Ĺ����У����ס��������乲ͬ�ӹ����810�����ʱ����׳���ӹ���ʱ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
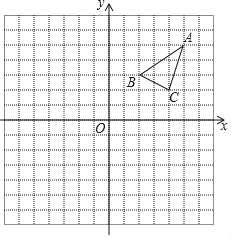
����Ŀ����֪��ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��
��1���Ȼ�����ABC����x��ԳƵ�ͼ����A1B1C1���ٻ�����A1B1C1����y��ԳƵ�ͼ����A2B2C2��
��2��ֱ��д����A2B2C2����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ��
��![]() �ϵ�һ�㣬����
�ϵ�һ�㣬����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() =
=![]() ��
��

![]() ��֤��
��֤��![]() ��
��![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ��
��![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��4��AD��3��AB��AD ,BC��12��
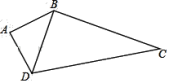
��1����BD�ij���
��2����CDΪ��ֵʱ����BDC����CDΪб�ߵ�ֱ�������Σ�
��3���ڣ�2���������£����ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��10��23�գ�����Ĵ�����ʽ��ͨ.����Ĵ��Ŷ�����ۿڰ��˹���������ֹ���麣���壬�ܳ�Լ55ǧ�ף������۰������״κ��������ij����Ϳ纣��ͨ����.10��24����ʽͨ�����죬����������ʿͬʱ����۹��ʻ�����������ۿڰ��˹�����������֪��������ʿ���ٶȱ���![]() ���Ұ�ʿ�ȼװ�ʿ��11���ӵ�����壬��������ƽ���ٶȸ��Ƕ���ǧ��/ʱ��
���Ұ�ʿ�ȼװ�ʿ��11���ӵ�����壬��������ƽ���ٶȸ��Ƕ���ǧ��/ʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
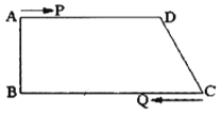
����Ŀ����ͼ�����ı���ABCD�У�AD//BC��![]() ��AD=24 cm��AB=8 cm, BC=26 cm������P��A��ʼ��AD����D��1cm/s���ٶ��˶���Q�ӵ�C��ʼ��CB����B��3 cm/s���ٶ��˶�.P��Q�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ������һ��Ҳ��ֹ֮ͣ�˶�.
��AD=24 cm��AB=8 cm, BC=26 cm������P��A��ʼ��AD����D��1cm/s���ٶ��˶���Q�ӵ�C��ʼ��CB����B��3 cm/s���ٶ��˶�.P��Q�ֱ�ӵ�A��Cͬʱ������������һ�㵽��˵�ʱ������һ��Ҳ��ֹ֮ͣ�˶�.
��1�����˶�ʱ��Ϊt��ʱ���ú�t�Ĵ���ʽ��ʾ�����߶εij��� AP=________, BQ=__________��
��2�����˶�ʱ��Ϊ������ʱ���ı���PQCDΪƽ���ı��Σ�
��3�����˶�ʱ��Ϊ������ʱ���ı���ABQPΪ���Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���BAD��ƽ���߽�CD�ڵ�G��AD��AE����AD��5��DE��6����AG�ij��ǣ�������

A. 6B. 8C. 10D. 12
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com