
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,且
,且![]() =
=![]() .
.

![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接OC,由![]() =
=![]() ,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
,根据圆周角定理得∠1=∠2,而∠1=∠OCA,则∠2=∠OCA,则可判断OC∥AD,由于AD⊥CD,所以OC⊥CD,然后根据切线的判定定理得到CD是⊙O的切线;
(2)连接BE交OC于F,由AB是⊙O的直径得∠ACB=90°.在Rt△ACB中,根据正切的定义得AC=4,再利用勾股定理计算出AB=5,然后证明Rt△ABC∽Rt△ACD,利用相似比先计算出AD=![]() ,再计算出CD=
,再计算出CD=![]() ;根据垂径定理的推论由
;根据垂径定理的推论由![]() =
=![]() 得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=
得OC⊥BE,BF=EF,于是可判断四边形DEFC为矩形,所以EF=CD=![]() ,则BE=2EF=
,则BE=2EF=![]() ,然后在Rt△ABE中,利用勾股定理计算出AE=
,然后在Rt△ABE中,利用勾股定理计算出AE=![]() ,再利用DE=AD﹣AE求解.
,再利用DE=AD﹣AE求解.
(1)连接OC,如图,∵![]() =
=![]() ,∴∠1=∠2.
,∴∠1=∠2.
∵OC=OA,∴∠1=∠OCA,∴∠2=∠OCA,∴OC∥AD.
∵AD⊥CD,∴OC⊥CD,∴CD是⊙O的切线;
(2)连接BE交OC于F,如图,∵AB是⊙O的直径,∴∠ACB=90°.在Rt△ACB中,tan∠CAB=![]() =
=![]() ,而BC=3,∴AC=4,∴AB=
,而BC=3,∴AC=4,∴AB=![]() =5.
=5.
∵∠1=∠2,∴Rt△ABC∽Rt△ACD,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,解得:AD=
,解得:AD=![]()
∵![]() =
=![]() ,即
,即![]() =
=![]() ,解得:CD=
,解得:CD=![]()
![]() =
=![]() ,∴OC⊥BE,BF=EF,∴四边形DEFC为矩形,∴EF=CD=
,∴OC⊥BE,BF=EF,∴四边形DEFC为矩形,∴EF=CD=![]() ,∴BE=2EF=
,∴BE=2EF=![]() .
.
∵AB为直径,∴∠BEA=90°.在Rt△ABE中,AE=![]() =
=![]() =
=![]() ,∴DE=AD﹣AE=
,∴DE=AD﹣AE=![]() ﹣
﹣![]() =
=![]() .
.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】有一个二次函数的图象,三位同学分别说出了它的一些特点:
甲:对称轴为直线x=4
乙:与x轴两个交点的横坐标都是整数.
丙:与y轴交点的纵坐标也是整数,且以这三个点为顶点的三角形面积为3.请你写出满足上述全部特点的一个二次函数解析式__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,与直线
,与直线![]() 交于点
交于点![]() .点
.点![]() 从点
从点![]() 出发以每秒1个单位的速度向点
出发以每秒1个单位的速度向点![]() 运动,运动时间设为
运动,运动时间设为![]() 秒.
秒.
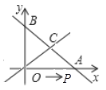
(1)求点![]() 的坐标;
的坐标;
(2)求下列情形![]() 的值;
的值;
①连结![]() ,
,![]() 把
把![]() 的面积平分;
的面积平分;
②连结![]() ,若
,若![]() 为直角三角形.
为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为宣传社会主义核心价值观,某社区居委会计划制作1200个大小相同的宣传栏.现有甲、乙两个广告公司都具备制作能力,居委会派出相关人员分别到这两个广告公司了解情况,获得如下信息:
信息一:甲公司单独制作完成这批宣传栏比乙公司单独制作完成这批宣传栏多用10天;
信息二:乙公司每天制作的数量是甲公司每天制作数量的1.2倍.
根据以上信息,求甲、乙两个广告公司每天分别能制作多少个宣传栏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在正方形网格中,若B(﹣3,﹣1),按要求回答下列问题:

(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出A和C的坐标;
(3)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热爱学习的小明同学在网上搜索到下面的文字材料:
在x轴上有两个点它们的坐标分别为(a,0)和(c,0).则这两个点所成的线段的长为|a﹣c|;同样,若在y轴上的两点坐标分别为(0,b)和(0,d),则这两个点所成的线段的长为|b﹣d|.如图1,在直角坐标系中的任意两点P1,P2,其坐标分别为(a,b)和(c,d),分别过这两个点作两坐标轴的平行线,构成一个直角三角形,其中直角边P1Q=|a﹣c|,P2Q=|b﹣d|,利用勾股定理可得:线段P1P2的长为![]() .
.
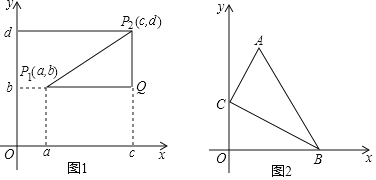
根据上面材料,回答下面的问题:
(1)在平面直角坐标系中,已知A(6,﹣1),B(6,5),则线段AB的长为 ;
(2)若点C在y轴上,点D的坐标是(﹣3,0),且CD=6,则点C的坐标是 ;
(3)如图2,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,求△ABC周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
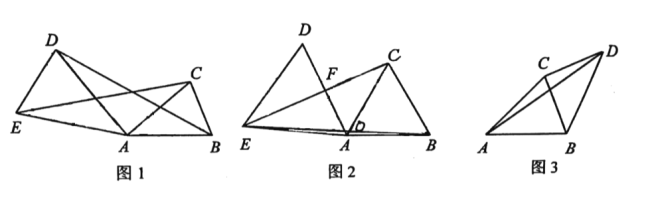
【题目】已知![]() 中,
中,![]() .
.
(1)如图1,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求证:
,求证:![]()
(2)如图2,在![]() 中,
中,![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
(3)如图3,在![]() 中,
中,![]() ,连接
,连接![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com