
【题目】如图,△ABC在正方形网格中,若B(﹣3,﹣1),按要求回答下列问题:

(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出A和C的坐标;
(3)求△ABC的周长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校计划建一间多功能数学实验室,将采购两类桌椅:A类是三角形桌,每桌可坐3人,B类是五边形桌,每桌可坐5人.学校拟选择甲、乙两家公司中的一家来采购,两家公司的标价均相同,且规定两类桌椅均只能在同一家公司采购.甲公司对两类桌椅均是以标价出售;乙公司对A类桌椅涨价20%、B类桌椅降价20%出售.经咨询,两家公司给出的数量和费用如下表:
A类桌椅(套) | B类桌椅(套) | 总费用(元) | |
甲公司 | 6 | 5 | 1900 |
乙公司 | 3 | 7 | 1660 |
(1)求第一次购买时,A、B两类桌椅每套的价格分别是多少?
(2)如果该数学实验室需设置48个座位,学校到甲公司采购,应分别采购A、B两类桌椅各多少套时所需费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是反比例函数![]() 上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为
上第一象限上一个动点,点A、点B为坐标轴上的点,A(0,k),B(k,0).已知△OAB的面积为![]() .
.
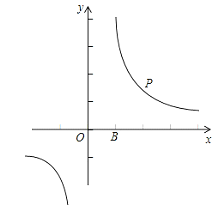
(1)求k的值;
(2)连接PA、PB、AB,设△PAB的面积为S,点P的横坐标为t.请直接写出S与t的函数关系式;
(3)阅读下面的材料回答问题:
当a>0时,![]()
∵![]() ≥0,∴
≥0,∴![]() ≥2,即
≥2,即![]() ≥2
≥2
由此可知:当![]() =0时,即a=1时,
=0时,即a=1时,![]() 取得最小值2.
取得最小值2.
问题:请你根据上述材料探索(2)中△PAB的面积S有没有最小值?若有,请直接写出S的最小值;若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为点B,AC⊥y轴,垂足为点C.
(1)写出点M的坐标;
(2)求直线MN的表达式;
(3)若点A的横坐标为-1,求矩形ABOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,垂足为点
,垂足为点![]() ,且
,且![]() ,连接
,连接![]() .
.
(1)如图①,求证:![]() 是等边三角形;
是等边三角形;

(2)如图①,若点![]() 、
、![]() 分别为
分别为![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:
,求证:![]() ;
;
(3)利用(1)(2)中的结论,思考并解答:如图②,![]() 为
为![]() 上一点,连结
上一点,连结![]() ,当
,当![]() 时,线段
时,线段![]() ,
,![]() ,
,![]() 之间有何数量关系,给出证明.
之间有何数量关系,给出证明.
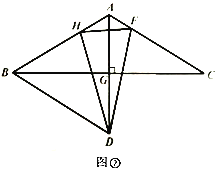
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com