
����Ŀ���ֳ�ѧϰ�⣺���ⱳ�����ڡ�ABC�У�AB��BC��AC���ߵij��ֱ�Ϊ![]() ��
��![]() ��
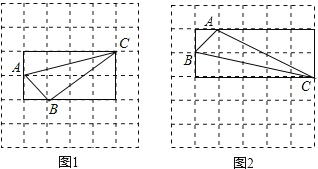
��![]() ������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ�������������ABC�ĸߣ�������������ܼ�������������
������������ε������С��ͬѧ�ڽ�������ʱ���Ƚ���һ������������ÿ��С�����εı߳�Ϊ1�������������л�������ABC������ABC�������㶼��С�����εĶ��㴦������ͼ1��ʾ�������������ABC�ĸߣ�������������ܼ�������������

��1�����㽫��ABC�����ֱ����д�ں����ϣ��� ��
˼ά��չ����2�����ǰ��������ABC����ķ���������ͼ��������ABC���ߵij��ֱ�Ϊ![]() ��
��![]() ��
��![]() ��a��0����������ͼ2������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC���������������ǣ��� ����
��a��0����������ͼ2������������ÿ��С�����εı߳�Ϊa��������Ӧ�ġ�ABC���������������ǣ��� ����
���𰸡���1��2.5����2����������3a2
��������
��1���ѡ�ABC���ڳ����λ����������þ��ε������ȥ��Χ���������ε��������
��2��![]() ��ֱ�DZ߳�Ϊa��a��ֱ�������ε�б�ߣ�
��ֱ�DZ߳�Ϊa��a��ֱ�������ε�б�ߣ�![]() ��ֱ�DZ߳�Ϊ4a��2a��ֱ�������ε�б�ߣ�
��ֱ�DZ߳�Ϊ4a��2a��ֱ�������ε�б�ߣ�![]() ��ֱ�DZ߳�Ϊa��5a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε������
��ֱ�DZ߳�Ϊa��5a��ֱ�������ε�б�ߣ���������Ϊһ�����ε������ȥ����ֱ�������ε������
��1��S��ABC��4��2��![]() ��4��1��
��4��1��![]() ��1��1��
��1��1��![]() ��2��3��2.5��
��2��3��2.5��
��2��S��ABC��5a��2a��![]() ��a��a��
��a��a��![]() ��2a��4a��
��2a��4a��![]() ��a��5a��3a2��
��a��5a��3a2��
�ʴ�Ϊ��2.5��3a2��


 ѧ���쳵��������������������ϵ�д�
ѧ���쳵��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
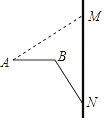
����Ŀ�����������ǵij��д����˼���ķ��㣮��ͼ������г���������г����κ����С��������ʱ��С�����֧�ܵĵ�N�����涥��M�ľ���MN=75cm���ҿ��Կ�������洹ֱ��չ��С����ʹ���汣��ˮƽ��AB��MN����MAB=��MNB=37������֧�ܳ�BN�������AB�ij���֮�͵���MN�ij��ȣ���С��������Ŀ���AB�������ȷ��1cm���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������OABC�Ķ���A��x���ϣ�����C��y���ϣ�OA��18��OC��12��D��E�ֱ�ΪOA��BC�ϵ����㣬��������OABC��ֱ��DE�۵���A�պ����C�غϣ���B���ڵ�F�����ٽ����չƽ��
��1����B���������� ����
��2����ֱ��DE�ĺ�������ʽ��
��3���趯��P�ӵ�D��������1����λ����/����ٶ�������D��A��B��C���յ�C�˶����˶�ʱ��Ϊt�룬��S��PDE��2S��OCDʱt��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
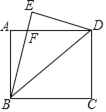
����Ŀ����ͼ��������ABCD�ضԽ���BD�۵���ʹ��C���ڵ�E����BE��AD���ڵ�F��
��1����֤����ABF�ա�EDF��
��2����AB=6��BC=8����AF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
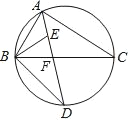
����Ŀ����ͼ����BAC��ƽ���߽�AABC�����Բ�ڵ�D����BC�ڵ�F����ABC��ƽ���߽�AD�ڵ�E��
��1����֤��DE=DB.
��2������BAC=90�㣬BD=4������ABC���Բ�İ뾶��
��3����BD=6��DF=4����AD�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪P��Q�ֱ��ǡ�O���ڽ���������ABCDEF�ı�AB��BC�ϵĵ㣬AP=BQ�����POQ�Ķ���Ϊ___�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A(n��-2)��B(1��4)��һ�κ���y=kx+b��ͼ��ͷ���������y=![]() ��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
��ͼ����������㣬ֱ��AB��y�ύ�ڵ�C��
(1)����������һ�κ����Ĺ�ϵʽ��
(2)����AOC�������
(3)��ʽkx+b-![]() <0�Ľ⼯(ֱ��д����)��
<0�Ľ⼯(ֱ��д����)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺
Ϊ�������������ļ�ֵ�ۣ�ij������ί��ƻ�����1200����С��ͬ�������������мס���������湫˾���߱�������������ί���ɳ������Ա�ֱ���������湫˾�˽���������������Ϣ��
��Ϣһ����˾������������������������ҹ�˾�������������������������10�죻
��Ϣ�����ҹ�˾ÿ�������������Ǽ�˾ÿ������������1.2����
����������Ϣ����ס���������湫˾ÿ��ֱ����������ٸ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A����4��![]() ����B����1��m����һ�κ���y=kx+b�뷴��������y=
����B����1��m����һ�κ���y=kx+b�뷴��������y=![]() ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
ͼ����������㣬AC��x���ڵ�C��BD��y���ڵ�D��
��1����m��ֵ��һ�κ�������ʽ��
��2��P���߶�AB�ϵ�һ�㣬����PC��PD������PCA����PDB�����ȣ����P���꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com