
【题目】如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.
(1)求证:△AFG∽△AED
(2)若FG=2,G为AD中点,求CG的长.
【答案】
(1)证明:∵AD是BC边上的中线,点E是BF中点,
∴BD=CD,BE=EF,
∴DE是△BCF的中位线,
∴DE∥CF,
∴DE∥FG,
∴△AFG∽△AED
(2)解:∵G为AD中点,FG∥DE,
∴AF=EF,
∴FG是△ADE的中位线,
∴DE=2FG=4,
∴CF=2DE=8,
∴CG=FC﹣FG=8﹣2=6
【解析】(1)在△BCF中,D是BC的中点,E,是BF的中点,故DE是△BCF的中位线,根据中位线定理得出DE∥CF,然后根据平行于三角形一边的直线截其它两边,所截得的三角形与原三角形相似,判断出△AFG∽△AED;
(2)根据中位线的判定由G为AD中点,FG∥DE,从而得出AF=EF,进而判断出FG是△ADE的中位线,根据中位线定理得出DE=2FG=4,CF=2DE=8,进而得出CG的长。
【考点精析】掌握三角形中位线定理和相似三角形的判定是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,n),且与直线y=﹣n始终保持相切,则n=(用含a的代数式表示).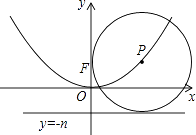
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车在刹车后行驶的距离s(单位:米)与时间t(单位:秒)之间的关系得部分数据如下表:
时间t(秒) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | … |
行驶距离s(米) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | … |
假设这种变化规律一直延续到汽车停止.
(1)根据这些数据在给出的坐标系中画出相应的点;
(2)选择适当的函数表示s与t之间的关系,求出相应的函数解析式;
(3)①刹车后汽车行驶了多长距离才停止? ②当t分别为t1 , t2(t1<t2)时,对应s的值分别为s1 , s2 , 请比较 ![]() 与
与 ![]() 的大小,并解释比较结果的实际意义.
的大小,并解释比较结果的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC:AB的值为 . 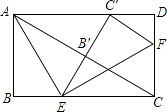
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列证明过程.
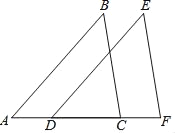
如图,已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
证明:∵AB∥DE
∴∠_____=∠_____(_______)
∵AD=CF
∴AD+DC=CF+DC即_____
在△ABC和△DEF中AB=DE_____
∴△ABC≌△DEF_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=60°,D是AC上一点,DE⊥AB于E,且CD=2,DE=1,则BC的长为( )
A.2
B.![]()
C.2 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,初三一班数学兴趣小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°.朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度为1: ![]() (即AB:BC=1:
(即AB:BC=1: ![]() ),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
),且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测量器的高度忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com