
【题目】如图①,若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,(点
上,(点![]() 与点
与点![]() 不重合),我们把这样的两条抛物线
不重合),我们把这样的两条抛物线![]() 和
和![]() ,互称为“友好”抛物线.
,互称为“友好”抛物线.
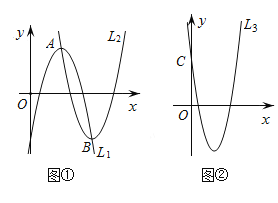
(1)一条抛物线的“友好”抛物线有 条;
(2)如图②,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 关于抛物线
关于抛物线![]() 的对称轴的对称点为点
的对称轴的对称点为点![]() ,求以点
,求以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的表达式;
的表达式;
(3)若抛物线![]() 的“友好”抛物线的解析式为
的“友好”抛物线的解析式为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系式.
的关系式.
【答案】(1)无数;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题目给的定义即可判断一条抛物线有无数条”友好”抛物线.
(2)先设出L4的解析式,求出L3的坐标轴和顶点坐标,再将顶点坐标代入L4的解析式中即可求解.
(3)根据两个抛物线的顶点都在对方抛物线上,列式求解即可.
(1)根据“友好”抛物线的定义,只需要确定原函数顶点和抛物线任意一点做“友好”抛物线的顶点即可作出“友好”抛物线,因此有无数条.
∴答案为:无数.
(2)把![]() 化为顶点式,得
化为顶点式,得
![]()
![]() 顶点坐标为
顶点坐标为![]() ,
,
对称轴为![]()
![]() 点坐标为
点坐标为![]() ,
,
![]() 点关于对称轴
点关于对称轴![]() 的对称点的坐标为
的对称点的坐标为![]() ,
,
设![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入,得
代入,得
![]() .
.
解得![]() .
.
![]() 的“友好”抛物线
的“友好”抛物线![]() 的表达式为:
的表达式为:![]() .
.
(3)由题意可得: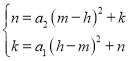 ,整理得,(a1+a2)(m-h)2=0,
,整理得,(a1+a2)(m-h)2=0,
∵顶点不重合,∴m≠h,
∴![]() .
.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论
①2a﹣b=0;
②a+b+c=0;
③当m≠﹣1时,a﹣b>am2+bm;
④当△ABC是等腰直角三角形时,a=![]() ;
;
⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为3![]() ,其中,正确的个数为( )
,其中,正确的个数为( )
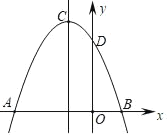
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
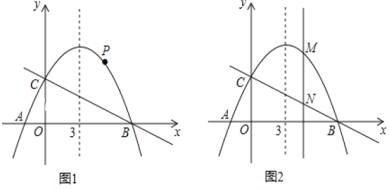
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,

(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM~△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,PM⊥PA交AC于点M,![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,AD:BC:AC=2:3:5,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程 (m-1)x![]() -mx+1=0。
-mx+1=0。
(1)证明:不论m为何值时,方程总有实数根;
(2)若m为整数,当m为何值时,方程有两个不相等的整数根。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD⊥BC,OE⊥BC,若∠BAC=45°.
(1)求证:OE=![]() BC;
BC;
(2)将△ACD沿AC折叠为△ACF,将△ABD沿AB折叠为△ABG,延长FC和GB相交于点H,若BD=6,CD=4,求AD的长;
(3)作OM⊥AB于M,ON⊥AC于N,在(2)的条件下求![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com