
【题目】在△ABC中,∠ABC=90°,

(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM~△BCN;
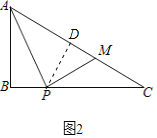
(2)如图2,P是边BC上一点,∠BAP=∠C,PM⊥PA交AC于点M,![]() =
=![]() ,求
,求![]() 的值;
的值;
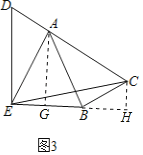
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,AD:BC:AC=2:3:5,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据同角的余角相等得到∠MAB=∠NBC,根据两角对应相等的两个三角形相似证明结论;
(2)过点P作PD⊥AM于D.证明△PDM∽△APM,根据相似三角形的性质得到![]() ,设DM=2a,根据勾股定理求出PM,证明△CDP∽△CBA,根据相似三角形的性质解答即可;
,设DM=2a,根据勾股定理求出PM,证明△CDP∽△CBA,根据相似三角形的性质解答即可;
(3)根据平行线的性质得到![]() ,根据相似三角形的性质得到
,根据相似三角形的性质得到![]() ,设BG=4m,AG=4n,根据
,设BG=4m,AG=4n,根据![]() 求出n=2m,计算即可.
求出n=2m,计算即可.
(1)证明:∵AM⊥MN,
∴∠MAB+∠MBA=90°,
∵∠ABC=90°,
∴∠CBN+∠MBA=90°,
∴∠MAB=∠NBC,又∠AMB=∠BNC=90°,
∴△ABM~△BCN;
(2)解:过点P作PD⊥AM于D.
∴∠BAP+∠APB=∠CPM+∠APB=90°,
∴∠BAP=∠CPM=∠C,
∴MP=MC,
∵PM⊥PA,PD⊥AM,
∴△PDM∽△APM,
∵![]()
设DM=2a,则![]()
由勾股定理得,![]()
∴CD=DM+CM=DM+PM=5a
则![]()
∵∠CDP=∠CBA=90°,∠C=∠C,
∴△CDP∽△CBA,
∴![]()
(3)解:过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,
∵∠DEB=90°,
∴CH∥AG∥DE,
∴![]()
∵BC:AC=3:5,
∴BC:AB=3:4,
由(1)可知,△ABG∽△BCH,
∴![]()
设BG=4m,CH=3m,AG=4n,BH=3n,
∵AB=AE,AG⊥BE,
∴EG=BG=4m,
∴GH=BG+BH=4m+3n,
∵![]()
∴![]()
解得,n=2m,
AG=4n=8m,BH=3n=6m,
由勾股定理得![]()
BE=2BG=8m,
∴![]()


 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
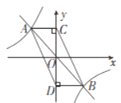
【题目】如图,函数y=-x与函数y=-![]() 的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
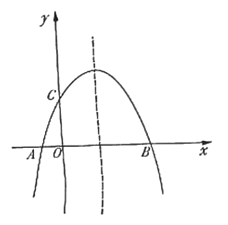
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,与
的右侧,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 在抛物线的对称轴上有一点
在抛物线的对称轴上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
![]() 点
点![]() 为
为![]() 轴上一动点,在抛物线上是否存在一点
轴上一动点,在抛物线上是否存在一点![]() ,使以
,使以![]() 四点构成的四边形为平行四边形?若存在,求点
四点构成的四边形为平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,若抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,抛物线
上,抛物线![]() 的顶点
的顶点![]() 在抛物线
在抛物线![]() 上,(点
上,(点![]() 与点
与点![]() 不重合),我们把这样的两条抛物线
不重合),我们把这样的两条抛物线![]() 和
和![]() ,互称为“友好”抛物线.
,互称为“友好”抛物线.
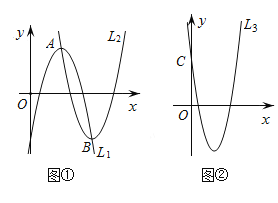
(1)一条抛物线的“友好”抛物线有 条;
(2)如图②,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 关于抛物线
关于抛物线![]() 的对称轴的对称点为点
的对称轴的对称点为点![]() ,求以点
,求以点![]() 为顶点的
为顶点的![]() 的“友好”抛物线
的“友好”抛物线![]() 的表达式;
的表达式;
(3)若抛物线![]() 的“友好”抛物线的解析式为
的“友好”抛物线的解析式为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的关系式.
的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
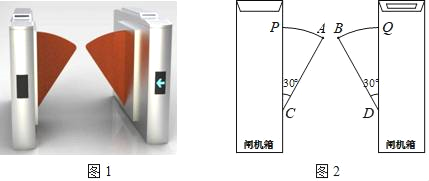
A. (54![]() +10) cm B. (54
+10) cm B. (54![]() +10) cm C. 64 cm D. 54cm
+10) cm C. 64 cm D. 54cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,Rt△ABC的内切圆⊙O,切点分别为点D、E、F,
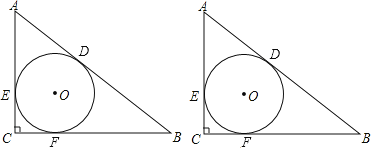
(1)若AC=3,BC=4,求△ABC的内切圆半径;
(2)当AD=5,BD=7时,求△ABC的面积;
(3)当AD=m,BD=n时,直接写出求△ABC的面积(用含m,n的式子表示)为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com