
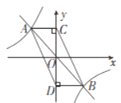
【题目】如图,函数y=-x与函数y=-![]() 的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.

(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A、B两种货物运输业务,已知3月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;4月份由于工人工资上涨,运费单价上涨情况为:A货物运费单价增加了40%,B货物运费单价上涨到40元/吨;该物流公司4月承接的A种货物和B种货物的数量与3月份相同,4月份共收取运费13000元.试求该物流公司3月份运输A、B两种货物各多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一个动点(不与点
上一个动点(不与点![]() 重合),连接
重合),连接![]() 过点
过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() .作
.作![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
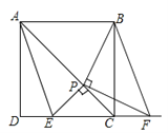
(1)由题意易知,![]() ,观察图,请猜想另外两组全等的三角形
,观察图,请猜想另外两组全等的三角形![]()
![]() ;
;![]()
![]() ;
;
(2)求证:四边形![]() 是平行四边形;
是平行四边形;
(3)已知![]() ,
,![]() 的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2-2m2x+2交y轴于点A,交直线x=4于点B.
(1)抛物线的对称轴为x=____________(用含m的代数式表示)
(2)若AB∥x轴,求抛物线的解析式.
(3)记抛物线在A、B之间的部分为图象G(包含A、B两点),若对于图象G上任意一点P(xp,yp),都有yp≤2,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《孙子算经》是唐初作为“算学”教科书的著名的《算经十书》之一,共三卷,上卷叙述算筹记数的制度和乘除法则,中卷举例说明筹算分数法和开平方法,都是了解中国古代筹算的重要资料,下卷收集了一些算术难题,“鸡兔同笼”便是其中一题.下卷中还有一题,记载为:“今有甲乙二人,持钱各不知数.甲得乙中半,可满四十八;乙得甲太半,亦满四十八.问甲、乙二人持钱各几何?”意思是:“甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文.如果乙得到甲所有钱的![]() ,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
,那么乙也共有钱48文.问甲、乙二人原来各有多少钱?”设甲原有钱x文,乙原有钱y文,可得方程组( )
A.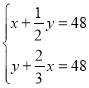 B.
B.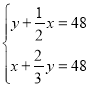 C.
C.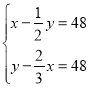 D.
D.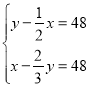
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°,

(1)如图1,分别过A,C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM~△BCN;
(2)如图2,P是边BC上一点,∠BAP=∠C,PM⊥PA交AC于点M,![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,AD:BC:AC=2:3:5,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com