
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,过点
,过点![]() 的直线
的直线![]() 垂直于线段
垂直于线段![]() ,点
,点![]() 是直线
是直线![]() 上在第一象限内的一动点,过点
上在第一象限内的一动点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,把
,把![]() 沿
沿![]() 翻折
翻折![]() ,使点
,使点![]() 落在点
落在点![]() 处,若以
处,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与△ABP相似,则满足此条件的点
为顶点的三角形与△ABP相似,则满足此条件的点![]() 的坐标为__________.
的坐标为__________.

【答案】![]() 或
或![]()
【解析】
求出直线l的解析式,证出△AOB∽△PCA,得出![]() ,设AC=m(m>0),则PC=2m,根据△PCA≌△PDA,得出
,设AC=m(m>0),则PC=2m,根据△PCA≌△PDA,得出 ![]() ,当△PAD∽△PBA时,根据
,当△PAD∽△PBA时,根据![]() ,
,![]() ,得出m=2,从而求出P点的坐标为(4,4)、(0,-4),若△PAD∽△BPA,得出
,得出m=2,从而求出P点的坐标为(4,4)、(0,-4),若△PAD∽△BPA,得出![]() ,求出
,求出![]() ,从而得出
,从而得出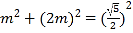 ,求出
,求出![]() ,即可得出P点的坐标为
,即可得出P点的坐标为![]() .
.
∵点A(2,0),点B(0,1),
∴直线AB的解析式为y=-![]() x+1
x+1
∵直线l过点A(4,0),且l⊥AB,
∴直线l的解析式为;y=2x-4,∠BAO+∠PAC=90°,
∵PC⊥x轴,
∴∠PAC+∠APC=90°,
∴∠BAO=∠APC,
∵∠AOB=∠ACP,
∴△AOB∽△PCA,
∴![]() ,
,
∴![]() ,
,
设AC=m(m>0),则PC=2m,
∵△PCA≌△PDA,
∴AC=AD,PC=PD,
∴![]() ,
,
如图1:当△PAD∽△PBA时,
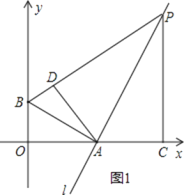
则![]() ,
,
则![]() ,
,
∵AB=![]() ,
,
∴AP=2![]() ,
,
∴![]() ,
,
∴m=±2,(负失去)
∴m=2,
当m=2时,PC=4,OC=4,P点的坐标为(4,4),
如图2,若△PAD∽△BPA,
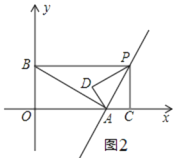
则![]() ,
,
∴![]() ,
,
则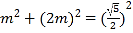 ,
,
∴m=±![]() ,(负舍去)
,(负舍去)
∴m=![]() ,
,
当m=![]() 时,PC=1,OC=
时,PC=1,OC=![]() ,
,
∴P点的坐标为(![]() ,1),
,1),
故答案为:P(4,4),P(![]() ,1).
,1).


科目:初中数学 来源: 题型:
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() ,P(a,b)是△ABC的边AC上一点:
,P(a,b)是△ABC的边AC上一点:
(1)将![]() 绕原点
绕原点![]() 逆时针旋转90°得到
逆时针旋转90°得到![]() ,请在网格中画出
,请在网格中画出![]() ,旋转过程中点A所走的路径长为 .
,旋转过程中点A所走的路径长为 .
(2)将△ABC沿一定的方向平移后,点P的对应点为P2(a+6,b+2),请在网格画出上述平移后的△A2B2C2,并写出点A2、的坐标:A2( ).
(3)若以点O为位似中心,作△A3B3C3与△ABC成2:1的位似,则与点P对应的点P3位似坐标为 (直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
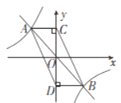
【题目】如图,函数y=-x与函数y=-![]() 的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
的图象相交于A、B两点,分别过A、B两点作y轴的垂线,垂足分别为点C、D,则四边形ACBD的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位数,记千位数字与百位数字之和为x,十位数字与个位数字之和为y,如果x=y,那么称这个四位数为“平衡数”.
(1)最小的“平衡数”为 ;四位数A与4738之和为最大的“平衡数”,则A的值为 ;
(2)一个四位“平衡数”M,它的个位数字是千位数字a的3倍,百位数字与十位数字之和为8,且千位数字a使得二次函数y=(a﹣2)x2﹣(2a﹣3)x+a﹣3与x轴有两个交点,求出所有满足条件的“平衡数”M的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为节能减排,某公交公司计划购买A型和B型两种环保节能公交车共10辆,若购买A型公交车2辆,B型公交车3辆,共需650万元;若购买A型公交车3辆,B型公交车2辆,共需600万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于830万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() 的图象交于A(a,-2),B两点.
的图象交于A(a,-2),B两点.
(1)求反比例函数的表达式和点B的坐标;
(2)P是第一象限内反比例函数图象上一点,过点P作y轴的平行线,交直线AB于点C,连接PO,若△POC的面积为3,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
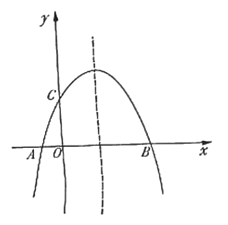
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点,点
两点,点![]() 在点
在点![]() 的右侧,与
的右侧,与![]() 轴相交于点
轴相交于点![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 在抛物线的对称轴上有一点
在抛物线的对称轴上有一点![]() ,使
,使![]() 的值最小,求点
的值最小,求点![]() 的坐标;
的坐标;
![]() 点
点![]() 为
为![]() 轴上一动点,在抛物线上是否存在一点
轴上一动点,在抛物线上是否存在一点![]() ,使以
,使以![]() 四点构成的四边形为平行四边形?若存在,求点
四点构成的四边形为平行四边形?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区各街道居民积极响应“创文明社区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A,B两个社区,B社区居民人口数量不超过A社区居民人口数量的2倍.
(1)求A社区居民人口至少有多少万人?
(2)街道工作人员调查A,B两个社区居民对“社会主义核心价值观”知晓情况发现:A社区有1.2万人知晓,B社区有1万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A社区的知晓人数平均月增长率为m%,B社区的知晓人数第一个月增长了m%,第二个月增长了2m%,两个月后,街道居民的知晓率达到76%,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应新旧动能转换.提高公司经济效益.某科技公司近期研发出一种新型高科技设备,每台设备成本价为30万元,经过市场调研发现,每台售价为40万元时,年销售量为600台;每台售价为45万元时,年销售量为550台.假定该设备的年销售量y(单位:台)和销售单价![]() (单位:万元)成一次函数关系.
(单位:万元)成一次函数关系.
(1)求年销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)根据相关规定,此设备的销售单价不得高于70万元,如果该公司想获得10000万元的年利润.则该设备的销售单价应是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com