
【题目】如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
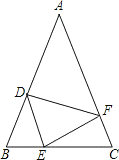
(1)求证:DE=EF;
(2)当∠A=44°时,求∠DEF的度数;
(3)当∠A等于多少度时,△DEF成为等边三角形?试证明你的结论.
【答案】(1)见解析(2)∠DEF=68°;(3)当∠A等于60度时,△DEF成为等边三角形,见解析.
【解析】
(1)根据AB=AC可得∠B=∠C,即可求证△BDE≌△CEF,即可解题;
(2)根据全等三角形的性质,得出∠BED=∠CFE,再根据三角形内角和定理以及平角的定义,即可求得∠DEF的度数;
(3)根据△DEF为等边三角形,以及△BDE≌△CEF,可得∠C的度数,最后根据等腰三角形ABC,求得其顶角的度数.
解:(1)∵AB=AC,
∴∠B=∠C,
∵在△BDE和△CEF中,
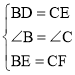 ,
,
∴△BDE≌△CEF(SAS),
∴DE=EF;
(2)当∠A=44°时,∠B=∠C=![]() (180°﹣44°)=68°,
(180°﹣44°)=68°,
∵△BDE≌△CEF,
∴∠BED=∠CFE,
∵△CEF中,∠CEF+∠CFE=180°﹣68°=112°,
∴∠BED+∠CEF=112°,
∴∠DEF=180°﹣112°=68°;
(3)当∠A等于60度时,△DEF成为等边三角形.
证明:若△DEF为等边三角形,则∠DEF=60°,
∴∠BED+∠CEF=120°,
又∵△BDE≌△CEF,
∴∠BED=∠CFE,
∴△CEF中,∠CEF+∠CFE=120°,
∴∠C=180°﹣120°=60°=∠B,
∴△ABC中,∠A=180°﹣60°×2=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
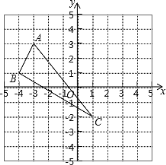
【题目】在平面直角坐标系中,△ABC三个顶点的位置如图(每个小正方形的边长均为1):
(1)请画出△ABC沿![]() 轴向右平移3个单位长度,再沿
轴向右平移3个单位长度,再沿![]() 轴向上平移2个单位长度后的
轴向上平移2个单位长度后的![]() (其中
(其中![]() 分别是A、B、C的对应点,不写画法);
分别是A、B、C的对应点,不写画法);
(2)直接写出![]() 三点的坐标;
三点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
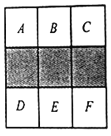
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列计算过程,猜想立方根.
![]() =1
=1 ![]() =8
=8 ![]() =27
=27 ![]() =64
=64 ![]() =125
=125 ![]() =216
=216 ![]() =343
=343 ![]() =512
=512 ![]() =729
=729
(1)小明是这样试求出19683的立方根的,先估计19683的立方根的个位数, 猜想它的个位数为 , 又由![]() <19000<
<19000< ![]() ,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
,猜想19683的立方根十位数为 ,验证得19683的立方根是 .
(2)请你根据(1)中小明的方法,完成如下填空:
① ![]() = ; ②
= ; ②![]() = ;③
= ;③![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道![]() 有以下两个方案:
有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最![]() 短在途中标出M、N的位置,保留画图痕迹;
短在途中标出M、N的位置,保留画图痕迹;

设方案一中铺设的支管道总长度为L1![]() ,方案二中铺设的支管道总长度为
,方案二中铺设的支管道总长度为![]() ,则L1与L2的大小关系为: L1_____ L2(填
,则L1与L2的大小关系为: L1_____ L2(填![]() ”、
”、![]() ”或)理由是______.
”或)理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
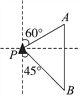
【题目】如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处与灯塔P的距离约为_______nmile.(结果取整数,参考数据:![]() =1.7,
=1.7, ![]() ≈ 1.4)
≈ 1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将连续的奇数1,3,5,7,9,…排成如图所示的数表,用一个“![]() ”形框框住任意七个数.
”形框框住任意七个数.
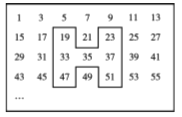
(1)若“![]() ”形框中间的奇数为
”形框中间的奇数为![]() ,那么框中的七个数之和用含
,那么框中的七个数之和用含![]() 的代数式可表示为_______;
的代数式可表示为_______;
(2)若落在“![]() ”形框中间且又是第二列的奇数17,31,45,…,则这一列数可以用代数式表示为
”形框中间且又是第二列的奇数17,31,45,…,则这一列数可以用代数式表示为![]() (
(![]() 为正整数),同样,落在“
为正整数),同样,落在“![]() ”形框中间又是第三列的奇数可表示为______(用含
”形框中间又是第三列的奇数可表示为______(用含![]() 的代数式表示);
的代数式表示);
(3)被“![]() ”形框框住的七个数之和能否等于1057?如果能,请求出中间的奇数,并直接说明这个奇数落在从左往右的第几列;如果不能,请写出理由.
”形框框住的七个数之和能否等于1057?如果能,请求出中间的奇数,并直接说明这个奇数落在从左往右的第几列;如果不能,请写出理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com