
分析 根据例题列出不等式组,解不等式组即可得出答案.
解答 解:根据题意得$\left\{\begin{array}{l}{5x+1≥0}&{\;}\\{2x-3<0}&{\;}\end{array}\right.$或$\left\{\begin{array}{l}{5x+1≤0}\\{2x-3>0}\end{array}\right.$,
解不等式组$\left\{\begin{array}{l}{5x+1≥0}&{\;}\\{2x-3<0}&{\;}\end{array}\right.$得-$\frac{1}{5}$≤x<$\frac{3}{2}$,
解不等式组$\left\{\begin{array}{l}{5x+1≤0}\\{2x-3>0}\end{array}\right.$,得:不等式组无解,
∴不等式$\frac{5x+1}{2x-3}$≤0的解集为-$\frac{1}{5}$≤x<$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a>b,则2a>2b | B. | 若-2a<-2b,则a>b | ||
| C. | 若a-1<b-1,则a>b | D. | 若a>b,则-a-1<-b-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:| 组别 | 成绩x(分) | 频数(人数) | 频率 |
| 一 | 50≤x<60 | 2 | 0.04 |
| 二 | 60≤x<70 | 10 | 0.2 |
| 三 | 70≤x<80 | 14 | b |
| 四 | 80≤x<90 | a | 0.32 |
| 五 | 90≤x<100 | 8 | 0.16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 2014 | D. | 2015 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )
如图是王老师去公园锻炼及原路返回时离家的距离y(千米)与时间t(分钟)之间的函数图象,根据图象信息,下列说法正确的是( )| A. | 王老师去时所用的时间少于回家的时间 | |
| B. | 王老师去公园锻炼了40分钟 | |
| C. | 王老师去时走上坡路,回家时走下坡路 | |
| D. | 王老师去时速度比回家时速度慢 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b2=c2-a2 | B. | a:b:c=3:4:5 | C. | ∠C=∠A-∠B | D. | ∠A:∠B:∠C=3:4:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
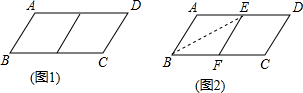
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com