
【题目】为提升青少年的身体素质,深圳市在全市中小学推行“阳光体育”活动,某学校为满足学生的需求,准备再购买一些篮球和足球,已知用800元购买篮球的个数比购买足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)如果计划用不多于5200元购买篮球、足球共60个,那么至少要购买多少个足球?
【答案】(1)100元/个, 80元/个.(2)40个
【解析】(1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,根据用800元购买篮球的个数比购买足球的个数少2个,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)购买m个足球,则购买(60﹣m)个篮球,根据总价=单价×购买数量结合总价钱不多于5200元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,取其内的最小正整数即可.
解:(1)设篮球的单价为x元/个,则足球的单价为0.8x元/个,
根据题意得:![]() +2=
+2=![]() ,
,
解得:x=100,
经检验,x=100是原方程的解,
∴0.8x=80.
答:篮球的单价为100元/个,足球的单价为80元/个.
(2)设购买m个足球,则购买(60﹣m)个篮球,
根据题意得:80m+100(60﹣m)≤5200,
解得:m≥40.
答:至少要购买40个足球.


科目:初中数学 来源: 题型:
【题目】如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )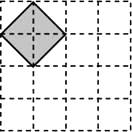
A.2种
B.3种
C.4种
D.5种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).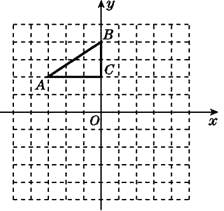
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标.
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣3经过A(﹣1,0)、B(3,0)两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标.
(3)如图②,直线y=![]() x+
x+![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
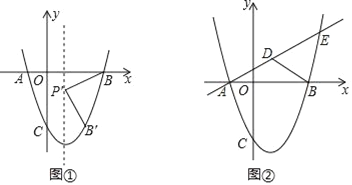
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△OAB中,OA=OB,C为AB中点,以O为圆心,OC长为半径作圆,AO与⊙O交于点E,直线OB与⊙O交于点F和D,连接EF、CF与OA交于点G.
(1)求证:直线AB是⊙O的切线;
(2)求证:ODEG=OGEF;
(3)若AB=8,BD=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E、F分别是AD及AD延长线上的点,且DE=DF,连接BF、CE.则下列结论中正确的有( )
①△BDF≌△CDE;②CE=BF;③ABD和△ACD的面积相等;④BF∥CE.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com