
【题目】已知抛物线y=ax2+bx﹣3经过A(﹣1,0)、B(3,0)两点,与y轴交于C点.
(1)求抛物线的解析式;
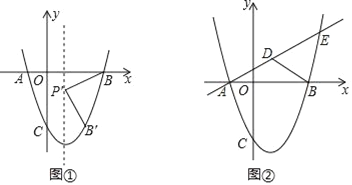
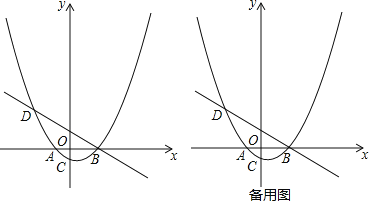
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标.
(3)如图②,直线y=![]() x+
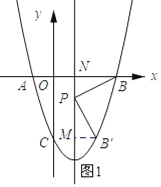
x+![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
【答案】(1)a=1,b=﹣2;(2)P(1,﹣1)(3)D(3,![]() ).
).
【解析】(1)将点A和点B的坐标代入抛物线的解析式可得到关于a、b的方程组,从而可求得a、b的值;
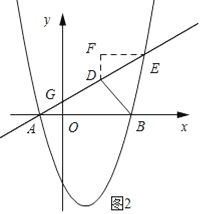
(2)先求得抛物线的对称轴为x=1.过点B′作B′M⊥对称轴,垂足为M.然后证明△BNP≌△PMB,依据全等三角形的性质可知BN=PM=3,PN=MB′.设P(1,m),则点B′的坐标为(1﹣m,m﹣2),最后将点B′的坐标代入抛物线的解析式求解即可;
(3)过点E作EF∥x轴,作点DF∥y轴,则∠EFD=90°.先求得点G的坐标,则可得到OG=![]() ,在Rt△AGO中,利用特殊锐角三角函数值可求得∠A的度数,则∠FED=30°,依据函数30°直角三角形的性质可得到DF=
,在Rt△AGO中,利用特殊锐角三角函数值可求得∠A的度数,则∠FED=30°,依据函数30°直角三角形的性质可得到DF=![]() DE.则动点Q沿DE以每秒2个单位的速度运动到E与它一每秒1个单位的速度运动东F所用时间相等.故此当BD+DF最短时,所用时间最短,依据两点之间线段最短可知当B,D,F在一条直线上时,所用时间最短,此时BE⊥BF,则点D的横坐标为3,然后由函数解析式再求得点D的纵坐标即可.
DE.则动点Q沿DE以每秒2个单位的速度运动到E与它一每秒1个单位的速度运动东F所用时间相等.故此当BD+DF最短时,所用时间最短,依据两点之间线段最短可知当B,D,F在一条直线上时,所用时间最短,此时BE⊥BF,则点D的横坐标为3,然后由函数解析式再求得点D的纵坐标即可.
解:(1)将点A和点B的坐标代入得:![]() ,
,
解得:a=1,b=﹣2.
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)∵A(﹣1,0),B(3,0),
∴抛物线的对称轴为x=1.
如图所示:过点B′作B′M⊥对称轴,垂足为M.
∵∠BPB′=90°,
∴∠BPN+∠B′PM=90°.
∵∠BPN+∠PBN=90°,
∴∠PNB=∠B′PM.
在△BPN和△PB′M中
∠PBN=∠B′PM,∠BNP=∠PM B′,PB=PB′,
∴△BNP≌△PMB.
∴BN=PM=3,PN=MB′.
设P(1,m),则点B′的坐标为(1﹣m,m﹣2).
将点B′的坐标代入抛物线的解析式得:
(1﹣m)2﹣2(1﹣m)﹣3=m﹣2,解得:m1=﹣1,m2=2.
∵点P在x轴的下方,
∴m=﹣1.
∴P(1,﹣1).
(3)存在.
如图所示:过点E作EF∥x轴,作点DF∥y轴,则∠EFD=90°.
将x=0代入直线AE的解析式得y=![]() ,
,
∴OG=![]() .
.
∴tan∠GAO=![]() .
.
∴∠FEA=∠GAO=30°.
∴DF=![]() DE.
DE.
∴动点Q沿DE以每秒2个单位的速度运动到E与它一每秒1个单位的速度运动东F所用时间相等.
∴当BD+DF最短时,所用时间最短.
∴当B,D,F在一条直线上时,所用时间最短.
∴点D的横坐标为3.
将x=3代入直线AE的解析式得:y=![]() .
.
∴D(3,![]() ).
).
“点睛”本题考查了二次函数图象的基本性质,最值问题及全等三角形性质,三角函数等知识点,对存在性问题进请说明理由难度适中,适合学生巩固知识.


科目:初中数学 来源: 题型:
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.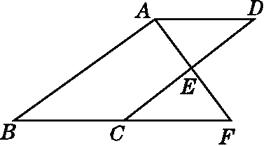
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):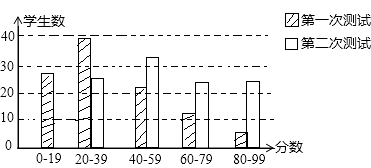
(1)两次测试最低分在第次测试中;
(2)第次测试成绩较好;
(3)第一次测试中,中位数在分数段,第二次测试中,中位数在分数段.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中有三个点A,B,C,要求作一个四边形,使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格纸的格点上.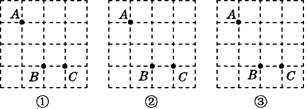
(1)在图①中作出的四边形是中心对称图形但不是轴对称图形;
(2)在图②中作出的四边形是轴对称图形但不是中心对称图形;
(3)在图③中作出的四边形既是轴对称图形又是中心对称图形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=8,AC=4,以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F,再分别以点E、F为圆心,大于EF长为半径画弧,两弧交于点G,作射线AG,交BC于点D,则D到AB的距离为( )
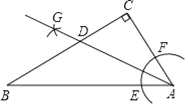
A. 2 B. 4 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提升青少年的身体素质,深圳市在全市中小学推行“阳光体育”活动,某学校为满足学生的需求,准备再购买一些篮球和足球,已知用800元购买篮球的个数比购买足球的个数少2个,足球的单价为篮球单价的![]() .
.
(1)求篮球、足球的单价分别为多少元?
(2)如果计划用不多于5200元购买篮球、足球共60个,那么至少要购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原创大型文化情感类节目《朗读者》在中央电视台综合频道、综艺频道播出后引起社会各界强烈反响,小明想了解本小区居民对《朗读者》的看法,进行了一次抽样调查,把居民对《朗读者》的看法分为四个层次:A.非常喜欢;B.较喜欢;C.一般;D.不喜欢;并将调查结果绘制了图1和图2两幅不完整的统计图.
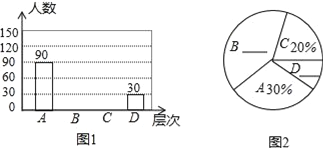
请你根据图中提供的信息解答下列问题:
(1)本次调查的居民总人数为=_____人;
(2)将图1和图2补充完整;
(3)图2中“C”层次所在扇形的圆心角的度数为_____;
(4)估计该小区4000名居民中对《朗读者》的看法表示喜欢(包括A层次和B层次)的大约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区便民超市为了了解顾客的消费情况,在该小区居民中进行调查,询问每户人家每周到超市的次数,下图是根据调查结果绘制的,请问:![]()
(1)这种统计图通常被称为什么统计图?
(2)此次调查共询问了多少户人家?
(3)超过半数的居民每周去多少次超市?
(4)请将这幅图改为扇形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() (a为常数,且a>0)与x轴从左至右
(a为常数,且a>0)与x轴从左至右
依次交于A,B两点,与y轴交于点C,经过点B的直线![]() 与抛物线的另一交
与抛物线的另一交
点为D,且点D的横坐标为﹣5.
(1)求抛物线的函数表达式;
(2)P为直线BD下方的抛物线上的一点,连接PD、PB, 求△PBD面积的最大值.
(3)设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com