
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.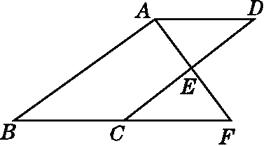
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
【答案】
(1)证明:在ABCD中,AD∥BC,
∴∠D=∠DCF.
∵点E是DC的中点
∴DE=CE
在△ADE和△FCE中,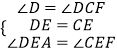
∴△ADE≌△FCE(ASA)
(2)解:由(1)知△ADE≌△FCE,
∴AD=CF=BC=5,
EF=AE=3.
∴BF=10,AF=6.
在Rt△BAF中,AB= ![]() =8,∴CD=AB=8
=8,∴CD=AB=8
【解析】(1)根据平行四边形的性质得出AD∥BC,就可证得∠D=∠DCF,再根据中点的定义可证得DE=CE,然后再根据全等三角形的判定证明△ADE≌△FCE即可。
(2)根据全等三角形的性质证明AD=CF=BC,根据BC的长求出BF的长,再根据AF=2EF求出AF的长,然后在Rt△BAF中,利用勾股定理求出AB的长,就可得出CD的长。


 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某地2017年第一季度财政收入为41.76亿元,用科学记数法表示为( )元
A.4176×105B.4.176×10 9C.4.176×10 8D.41.76×10 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线![]() 与
与![]() 满足
满足![]() ,则称
,则称![]() 互为“相关抛物线”给出如下结论:
互为“相关抛物线”给出如下结论:
①y1与y2的开口方向,开口大小不一定相同; ②y1与y2的对称轴相同;③若y2的最值为m,则y1的最值为k2m;④若函数![]() 与x 轴的两交点间距离为d,则函数
与x 轴的两交点间距离为d,则函数![]() 与x 轴的两交点间距离也为
与x 轴的两交点间距离也为![]() .其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
.其中正确的结论的序号是___________(把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校随机抽查的20名八年级男生的身高统计表:
身高(cm) | 150 | 155 | 160 | 163 | 165 | 168 |
人数(人) | 1 | 3 | 4 | 4 | 5 | 3 |
这组数据的众数是cm,中位数是cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx﹣3经过A(﹣1,0)、B(3,0)两点,与y轴交于C点.
(1)求抛物线的解析式;
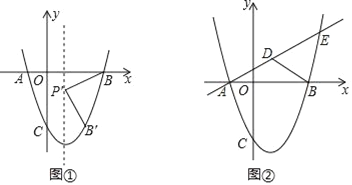
(2)如图①,抛物线的对称轴上有一点P,且点P在x轴下方,线段PB绕点P顺时针旋转90°,点B的对应点B′恰好落在抛物线上,求点P的坐标.
(3)如图②,直线y=![]() x+
x+![]() 交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
交抛物线于A、E两点,点D为线段AE上一点,连接BD,有一动点Q从B点出发,沿线段BD以每秒1个单位的速度运动到D,再沿DE以每秒2个单位的速度运动到E,问:是否存在点D,使点Q从点B到E的运动时间最少?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com