
����Ŀ����ͼ,��ƽ��ֱ������ϵ��,Rt��ABC����������ֱ���A(-3,2),B(0,4),C(0,2).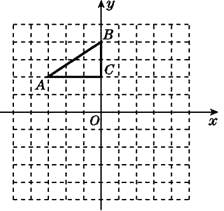
��1������ABC�Ե�CΪ��ת������ת180��,������ת���Ӧ�ġ�A1B1C;ƽ�ơ�ABC,����A�Ķ�Ӧ��A2������Ϊ(0,-4),����ƽ�ƺ��Ӧ�ġ�A2B2C2.
��2��������A1B1C��ijһ����ת���Եõ���A2B2C2,��ֱ��д����ת���ĵ�����.
��3����x������һ��P,ʹ��PA+PB��ֵ��С,��ֱ��д����P������.
���𰸡�
��1���⣺��ͼ��ʾ.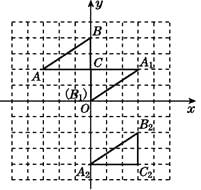
��2���⣺��ͼ������A1A2 �� CC2 �� A1A2��CC2�ཻ�ڵ�P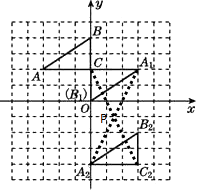
��ת���ĵ�����Ϊ��P��
A1��3,2����A2��0��-4��
��ֱ��A1A2�Ľ���ʽΪy1=kx+b![]() ,��֮�ã�
,��֮�ã�![]()
y1=2x-4
C��0,2����C2��3��-4��
��ֱ��CC2�Ľ���ʽΪy2=mx+n
��![]() ,��֮�ã�
,��֮�ã�![]()
��y2=-2x+2
��y1=y2
��2x-4=-2x+2
x=![]() ��y2=-1
��y2=-1
��P��![]() ��-1��
��-1��
����ת���ĵ�������P��![]() ��-1��
��-1��
��3���⣺��ͼ������A����x��ĶԳƵ�M������BM��x���ڵ�N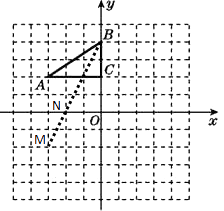
��M��-3��-2����B��0,4��
��ֱ��MB�Ľ���ʽΪy=kx+b![]() ,��֮�أ�
,��֮�أ�![]()
y=2x+4
y=0ʱ��2x+4=0����x=-2
�ʵ�P������Ϊ(-2,0)
����������1����������ṹ�ҳ���A��B��C��ת180���Ķ�Ӧ��A1��B1��C1��λ�ã�Ȼ��˳�����Ӽ��ɣ��ҳ�ƽ�ƺ�Ķ�Ӧ��A2��B2��C2��λ�ã�Ȼ��˳�����Ӽ��ɡ�
��2��������ת�Ķ�����ͼ�Σ�����A1A2 �� CC2 �� A1A2��CC2�ཻ�ڵ�P�������ֱ��A1A2��ֱ��CC2�ĺ�������ʽ��������������Ľ������꣬������ת���ĵ�P�����ꡣ
��2������A����x��ĶԳƵ�M������BM��x���ڵ�N�����ô���ϵ�������ֱ��MB�Ľ���ʽ���ٸ���y=0�������ɵó�P�����ꡣ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
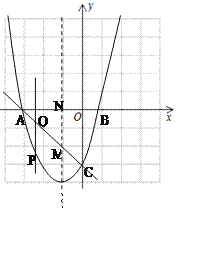
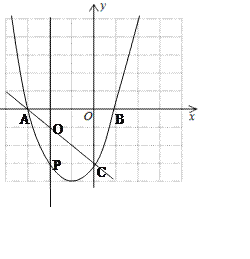
����Ŀ����ͼ��ʾ��һ�κ���![]() �ֱ�x��y����A��C���㣬������
�ֱ�x��y����A��C���㣬������![]() �뾭����A��C.
�뾭����A��C.
��1����������ߵĺ�������ʽ��
��2����PΪ��������A��C������һ�����㣬����P��ֱ��![]() ����ֱ��AC�ڵ�Q������P�˶���ʲôλ��ʱ���߶�PQ�ij�����������ȣ�����ʱP�����ꡣ
����ֱ��AC�ڵ�Q������P�˶���ʲôλ��ʱ���߶�PQ�ij�����������ȣ�����ʱP�����ꡣ
��3���ڣ�2�������£�ֱ��![]() ��
��![]() �ύ��N����ֱ��AC���ڵ�M����N��M��Q��D�ĵ���ƽ���ı���ʱ��ֱ��д��D������ꡣ
�ύ��N����ֱ��AC���ڵ�M����N��M��Q��D�ĵ���ƽ���ı���ʱ��ֱ��д��D������ꡣ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ֽ����������A,B,C,Ҫ����һ���ı���,ʹ��������������ı��εı�(��������)��,���ı��εĶ����ڷ���ֽ�ĸ����.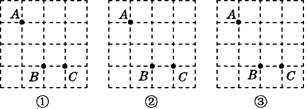
��1����ͼ�����������ı��������ĶԳ�ͼ�ε�������Գ�ͼ��;
��2����ͼ�����������ı�������Գ�ͼ�ε��������ĶԳ�ͼ��;
��3����ͼ�����������ı��μ�����Գ�ͼ���������ĶԳ�ͼ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
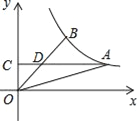
����Ŀ����ͼ��A��B�Ƿ���������![]() ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��
ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC��AC��OB�ڵ�D����DΪOB���е㣬��AOD�����Ϊ3����k��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������������������ʣ���������ȫ����Сѧ���С��������������ijѧУΪ����ѧ�����������ٹ���һЩ�����������֪��800Ԫ��������ĸ����ȹ�������ĸ�����2��������ĵ���Ϊ���۵�![]() ��
��
��1������������ĵ��۷ֱ�Ϊ����Ԫ��
��2������ƻ��ò�����5200Ԫ������������60������ô����Ҫ������ٸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽���꼶ѧ���Ŀ����Ķ��������У������Ӱ��꼶�����ȡ��������ѧ���������ǵĶ���ʱ������˵��鲢���ռ������ݻ����������������ͳ��ͼ����������ͼ���ṩ����Ϣ������������⣺��ÿ�麬��Сֵ�������ֵ��![]()
��1���Ӱ��꼶��ȡ�˶�����ѧ����
��2����գ�ֱ�ӰѴ�������ϣ�
�١�2-2.5Сʱ���IJ��ֶ�Ӧ������Բ�Ľ�Ϊ�ȣ�
�ڿ����Ķ�ʱ�����λ����������ʱ��Σ��ڣ�
��3��������꼶����800��ѧ�����������꼶ѧ�������Ķ�ʱ�䲻����1.5Сʱ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��˫����![]() �ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��
�ڵ�һ���ķ�֧�ϵ�һ�����㣬����AO���ӳ�����һ��
֧�ڵ�B����ABΪ�����ȱߡ�ABC����C�ڵ������ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����![]() (k��0)���˶�����k��ֵ��________��
(k��0)���˶�����k��ֵ��________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com