
【题目】如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.

(1)求证:△BOE≌△DOF;
(2)若![]() ,则四边形ABCD是什么特殊四边形?请说明理由.
,则四边形ABCD是什么特殊四边形?请说明理由.
【答案】(1)证明见解析;(2)解:四边形ABCD是矩形,理由见解析.
【解析】(1)根据AAS或ASA即可证明;(2)结论:矩形. 只要证明对角线AC=BD即可;
解: (1)∴ ∠BEO=90°=∠DFO ,
又∵ OE=OF ∠BOE=∠DOF,
∴ △BOE≌△DOF(ASA),
(2)解:四边形ABCD是矩形,
证明:∵ △BOE≌△DOF,
∴ OB=OD,
∵ OE=OF,CE=AF,
∴ OC=OA,
∴ 四边形ABCD是平行四边形,
∴![]() ,
,
又∵![]() ,
,
∴ AC=BD,
∴□ABCD是矩形.
“点睛”本题考查全等三角形的判定与性质、平行四边形的判定和性质. 矩形的判定和性质等知识,解题的关键是熟练掌握基本概念,灵活运用知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:
【题目】一名同学调查了全班![]() 名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
名同学分别喜欢相声、小品、歌曲、舞蹈节目的类别情况,并制成如下统计表:
最喜欢的节目类别 | 划记 | 人数 | 百分数(%) |
相声 | 正 |
|
|
小品 | 正正正一 |
|
|
歌曲 | 正正 |
|
|
舞蹈 | 正一 |
|
|
其中对这些节目类别的统计中,仅有一类节目的统计是完全正确的,该项统计类别是( )
A.相声B.小品C.歌曲D.舞蹈
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同),购买1个足球和2个篮球共需270元;购买2个足球和3个篮球共需440元.
(1)问足球和篮球的单价各是多少元?
(2)若购买足球和篮球共24个,且购买篮球的个数大于足球个数的2倍,购买球的总费用不超过2220元,问该学校有哪几种不同的购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=3x2+1和y=3(x﹣1)2 , 以下说法: ①它们的图象都是开口向上;
②它们的对称轴都是y轴,顶点坐标都是原点(0,0);
③当x>0时,它们的函数值y都是随着x的增大而增大;
④它们的开口的大小是一样的.
其中正确的说法有( )
A. 1个 B. 2 C. 3 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,点![]() 坐标
坐标![]() ,点
,点![]() 坐标
坐标![]() ,连接
,连接![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() .
.
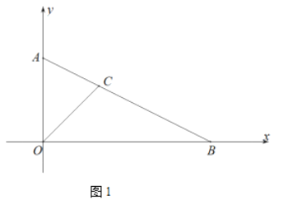
(1)如图1,求![]() 的长;
的长;
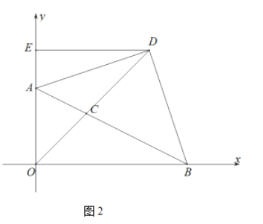
(2)如图2,![]() 是
是![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,若点
,若点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的关系;
的关系;
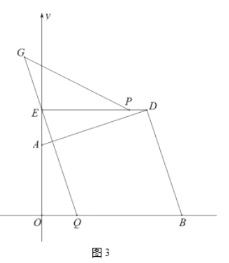
(3)在(2)的条件下,如图3,线段![]() 上存在一点
上存在一点![]() ,使得
,使得![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 值?
值?
查看答案和解析>>
科目:初中数学 来源: 题型:
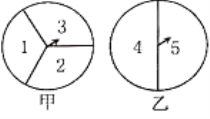
【题目】如图,甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.小夏和小秋利用它们来做决定获胜与否的游戏.规定小夏转甲盘一次、小秋转乙盘一次为一次游戏(当指针指在边界线上时视为无效,重转).
(1)小夏说:“如果两个指针所指区域内的数之和为6或7,则我获胜;否则你获胜”.按小夏设计的规则,请你写出两人获胜的可能性分别是多少?
(2)请你对小夏和小秋玩的这种游戏设计一种公平的游戏规则,并用一种合适的方法(例如:树状图,列表)说明其公平性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知点
中,已知点![]() ,
,![]() ,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________.
,请确定点C的坐标,使得以A,B,C,O为顶点的四边形是平行四边形,则满足条件的所有点C的坐标是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款386元,这两种商品原销售价之和为500元.问:这两种商品的原销售价分别为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com