

���� ��1�����ڶ��κ������κ���y=$\frac{3}{2}$x2-$\frac{9}{2}$x+3����x=0�õ�y=3����y=0���õ�$\frac{3}{2}$x2-$\frac{9}{2}$x+3=0�����x=1��2���ɵ�A��1��0����B ��2��0����C��0��3�����ɴ˼��ɽ�����⣮
��2��С���ķ����Ǵ���ģ�����ȫ�������ε����������D�����꣬���ж��Ƿ����������ϼ��ɣ�
��3����ͼ2�У��ֱ���A��BΪ�뾶1Ϊ�뾶��Բ����ֱ��y=kx+3���A����ʱ����A��B��PΪ����ĵ�������������ֻ��4��������е�P1�����꼴�ɽ�����⣮
��� �⣺��1�����ڶ��κ������κ���y=$\frac{3}{2}$x2-$\frac{9}{2}$x+3����x=0�õ�y=3����y=0���õ�$\frac{3}{2}$x2-$\frac{9}{2}$x+3=0�����x=1��2��
��A��1��0����B��2��0����C��0��3����
��OA=1��OB=2��OC=3��AB=1��
��S��ABC=$\frac{1}{2}$��1��3=$\frac{3}{2}$��
��2��С���ķ����Ǵ���ģ�
���ɣ���ͼ1�У�����AD��BC��H��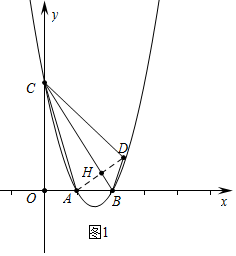
������ڵ�D��ʹ�á�ABC�ա�DBC����D��m��n����
��CA=CD��BA=BD��
��BC��ֱƽ���߶�AD��
��B��2��0����C��0��3����
��ֱ��BC�Ľ���ʽΪy=-$\frac{3}{2}$x+3��ֱ��AD�Ľ���ʽΪy=$\frac{2}{3}$x-$\frac{2}{3}$��
��$\left\{\begin{array}{l}{y=-\frac{3}{2}x+3}\\{y=\frac{2}{3}x-\frac{2}{3}}\end{array}\right.$�����$\left\{\begin{array}{l}{x=\frac{22}{13}}\\{y=\frac{6}{13}}\end{array}\right.$��
��H��$\frac{22}{13}$��$\frac{6}{13}$����
��AH=DH��
��$\frac{1+m}{2}$=$\frac{22}{13}$��$\frac{0+n}{2}$=$\frac{6}{13}$��
��m=$\frac{31}{13}$��n=$\frac{12}{13}$��
��D��$\frac{31}{13}$��$\frac{12}{13}$����
��x=$\frac{31}{13}$ʱ��y�T$\frac{3}{2}$•��$\frac{31}{13}$��2-$\frac{9}{2}$•$\frac{31}{13}$+3=$\frac{135}{169}$��
���D���������ߵ�ͼ���ϣ�
��С���ķ����Ǵ���ģ�
��3����ͼ2�У��ֱ���A��BΪ�뾶1Ϊ�뾶��Բ����ֱ��y=kx+3���A������P1ʱ����A��B��PΪ����ĵ�������������ֻ��4������ͼ�У���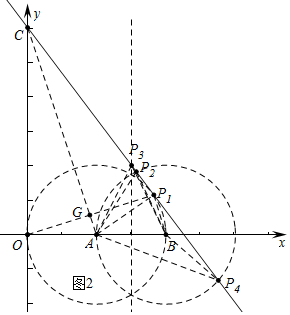
��CO=CP1��OA=AP1
��AC��ֱƽ���߶�OP1��
��ֱ��AC�Ľ���ʽΪy=-3x+3��ֱ��OP1�Ľ���ʽΪy=$\frac{1}{3}$x��
��$\left\{\begin{array}{l}{y=\frac{1}{3}x}\\{y=-3x+3}\end{array}\right.$���$\left\{\begin{array}{l}{x=\frac{9}{10}}\\{y=\frac{3}{10}}\end{array}\right.$��
��G��$\frac{9}{10}$��$\frac{3}{10}$����
��OG=GP1��
��P1��$\frac{9}{5}$��$\frac{3}{5}$��������y=kx+3�õ���k=-$\frac{4}{3}$��
������������k��ֵΪ-$\frac{4}{3}$��
���� ���⿼����κ����ۺ��⡢һ�κ�����Ӧ�á�ȫ�������ε��ж������ʡ�Բ���й�֪ʶ���߶εĴ�ֱƽ���ߵ��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ��ѧ�ṹ��һ�κ��������÷������е㽻�����꣬�����п�ѹ���⣮


 ��һ������Ԫͬ�����ؾ�ϵ�д�
��һ������Ԫͬ�����ؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��9 | B�� | m��9 | C�� | m��9 | D�� | m��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪����������y1=$\frac{k_1}{x}$��һ�κ���y2=k2x+b��ͼ���ڵ�A��1��8����B��-4��m�����㣮
��ͼ����֪����������y1=$\frac{k_1}{x}$��һ�κ���y2=k2x+b��ͼ���ڵ�A��1��8����B��-4��m�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
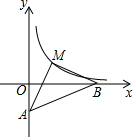 ��ͼ��ֱ��y=$\frac{1}{5}$x-1��x�ᡢy��ֱ��ཻ��B��A����MΪ˫����y=$\frac{k}{x}$��x��0����һ�㣬����AMB����ABΪ�ĵ���ֱ�������Σ���S��MAB��k��ֵ��
��ͼ��ֱ��y=$\frac{1}{5}$x-1��x�ᡢy��ֱ��ཻ��B��A����MΪ˫����y=$\frac{k}{x}$��x��0����һ�㣬����AMB����ABΪ�ĵ���ֱ�������Σ���S��MAB��k��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ȱ������� | B�� | ���������� | C�� | ֱ�������� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
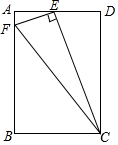 ��ͼ���ھ���ABCD�У�EΪAD��һ�㣬EF��EC��AB��F������FC����AEF���DCE�Ƿ����ƣ������˵����
��ͼ���ھ���ABCD�У�EΪAD��һ�㣬EF��EC��AB��F������FC����AEF���DCE�Ƿ����ƣ������˵�����鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com