
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边上的动点.
边上的动点.
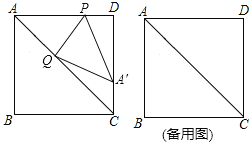
(1)AC等于多少;
(2)若![]() ,且点
,且点![]() 关于
关于![]() 的对称点
的对称点![]() 落在
落在![]() 边上,求
边上,求![]() 的值;
的值;
(3)设![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 与
与![]() 面积之和
面积之和![]() 的最小值.(用含
的最小值.(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 与
与![]() 面积之和
面积之和![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)由正方形的性质可得对角线的长,
(2)由点A与点A′关于PQ对称知△APQ与△A′PQ关于PQ对称,再证∠PA′D=∠A′QC,由AB=4,AP=3PD得PD=1,AP=PA′=3,A′D=2![]() ,利用正切函数的定义即可得答案,
,利用正切函数的定义即可得答案,
(3)过点Q作直线MN⊥AD于点M,交BC于点N,则MN⊥BC,证△APQ∽△CTQ得![]() =
=![]() ,设QM=h,则QN=4-h,CT=
,设QM=h,则QN=4-h,CT=![]() ,继而知S=
,继而知S=![]() ah+
ah+![]()
![]() (4-h),整理得ah2-(4a+S)h+8a=0,根据方程有实数根得(4a+S)2≥32a2,结合4a+S>0知S≥(4
(4-h),整理得ah2-(4a+S)h+8a=0,根据方程有实数根得(4a+S)2≥32a2,结合4a+S>0知S≥(4![]() -4)a,最后根据S=(4
-4)a,最后根据S=(4![]() -4)a时可得h=2
-4)a时可得h=2![]() .
.
解:(1)∵四边形ABCD是正方形,且AB=4,
∴AB=BC=4,∠BAC=∠ACB=45°,
∴AC=![]() =
=![]() =
=![]() ,
,
(2)如图1,
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
∴![]() .
.
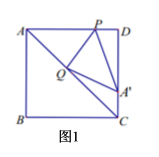
(3)如图2,过点![]() 作直线
作直线![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
整理得:![]() ,
,
∵关于![]() 的一元二次方程
的一元二次方程![]() 有实根,∴
有实根,∴![]() ,
,
∴![]() ,
,
![]() ,又
,又![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,由方程
时,由方程![]() 可得
可得![]() 满足题意,
满足题意,
故当![]() 时,
时,![]() 与
与![]() 面积之和
面积之和![]() 的最小值为
的最小值为![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
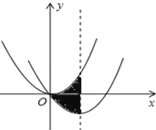
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A、B两个观测站,C离海岸线l的距离(即CD的长)为2,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则AB的长( )
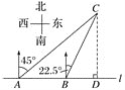
A. 2 km B. (2+![]() )km C. (4-2
)km C. (4-2![]() ) km D. (4-
) km D. (4-![]() ) km
) km
查看答案和解析>>
科目:初中数学 来源: 题型:
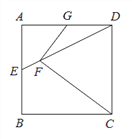
【题目】己知:如图,在正方形ABCD中,点E为边AB的中点,联结DE,点F在DE上CF=CD,过点F作FG⊥FC交AD于点G.
(1)求证:GF=GD;
(2)联结AF,求证:AF⊥DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件 30 元,售价为每件 40 元.每天可以销售 48 件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件 32.4 元,求两次下降的百分率;
(2) 经调查,若该商品每降价 0.5 元,每天可多销售 4 件,那么每天要想获得 510 元的利润,每件应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
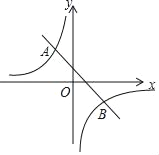
【题目】如图,已知A(m,2),B(2,n)是一次函数y=﹣x+1的图象与反比例函数y=![]() (k≠0)图象的两个交点.
(k≠0)图象的两个交点.
(1)求反比例函数的解析式;
(2)根据图象,请直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
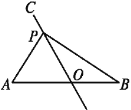
【题目】如图,某同学在一张硬纸板的中间画了一条4cm长的线段AB,过AB的中点O画直线CO,使∠AOC=60°,在直线CO上取一点P,作△PAB并剪下(纸板足够大),当剪下的△PAB为直角三角形时,AP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,D、E分别在边AB、AC上,下列条件中,不能确定△ADE∽△ACB的是( )
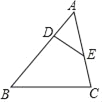
A. ∠AED=∠B B. ∠BDE+∠C=180°
C. ADBC=ACDE D. ADAB=AEAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com