
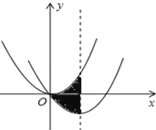
【题目】如图,在平面直角坐标系中,抛物线y=![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为![]() ,则a、b的值分别为( )
,则a、b的值分别为( )
A. ![]() ,
,![]() B.
B. ![]() ,﹣
,﹣![]() C.
C. ![]() ,﹣
,﹣![]() D. ﹣
D. ﹣![]() ,
,![]()
科目:初中数学 来源: 题型:
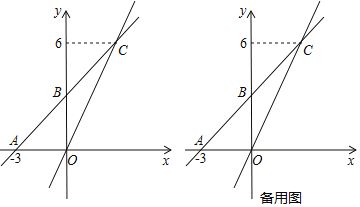
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与正比例函数
,且与正比例函数![]() 的图象交于点
的图象交于点![]() .
.
(1)求一次函数![]() 的解析式;
的解析式;
(2)点![]() 在
在![]() 轴上,当
轴上,当![]() 最小时,求出点
最小时,求出点![]() 的坐标;
的坐标;
(3)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是平面内一点,以
是平面内一点,以![]() 、
、![]() 、
、![]() 、
、![]() 四点为顶点的四边形是矩形,请直接写出点
四点为顶点的四边形是矩形,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校组织植树活动,已知在甲处植树的有220人,在乙处植树的有96人.
(1)若要使甲处植树的人数是乙处植树人数的3倍,应从乙处调多少人去甲处?
(2)为了尽快完成植树任务,现调m人去两处支援,其中![]() ,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
,若要使甲处植树的人数仍然是乙处植树人数的3倍,则应调往甲,乙两处各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
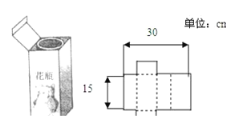
【题目】如图,将一个饮料包装盒剪开,铺平,纸样如图所示,包装盒的高为![]() ;设包装盒底面的长为
;设包装盒底面的长为![]() .
.
(1)用![]() 表示包装盒底面的宽;
表示包装盒底面的宽;
(2)用![]() 表示包装盒的表面积,并化简;
表示包装盒的表面积,并化简;
(3)若包装盒底面的长为![]() ,求包装盒的表面积.
,求包装盒的表面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
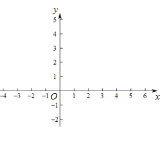
【题目】在平面直角坐标系中,直线![]() (
(![]() )与直线
)与直线![]() 相交于点P(2,m),与x轴交于点A.
相交于点P(2,m),与x轴交于点A.
(1)求m的值;
(2)过点P作PB⊥x轴于B,如果△PAB的面积为6,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
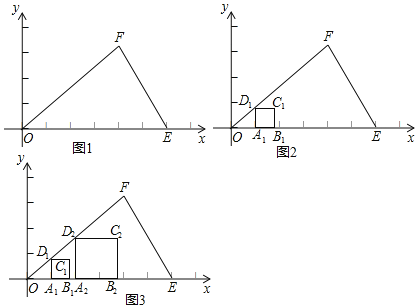
【题目】阅读以下内容并回答问题:
如图1,在平面直角坐标系xOy中,有一个△OEF,要求在△OEF内作一个内接正方形ABCD,使正方形A,B两个顶点在△OEF的OE边上,另两个顶点C,D分别在EF和OF两条边上.
小丽感到要使四边形的四个顶点同时满足上述条件有些困难,但可以先让四边形的三个顶点满足条件,于是她先画了一个有三个顶点在三角形边上的正方形(如图2).接着她又在△OEF内画了一个这样的正方形(如图3).她发现如果再多画一些这样的正方形,就能发现这些点C位置的排列图形,根据这个图形就能画出满足条件的正方形了.
(1)请你也实验一下,再多画几个这样的正方形,猜想小丽发现这些点C排列的图形是 ;
(2)请你参考上述思路,继续解决问题:如果E,F两点的坐标分别为E(6,0),F(4,3).
①当A1的坐标是(1,0)时,则C1的坐标是 ;
②当A2的坐标是(2,0)时,则C2的坐标是 ;
③结合(1)中猜想,求出正方形ABCD的顶点D的坐标,在图3中画出满足条件的正方形ABCD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com