
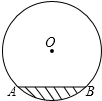
 如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少?
如图,水平放着的圆柱形水管的截面半径是12,其中水面的高为6,求水面AB的宽度是多少? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
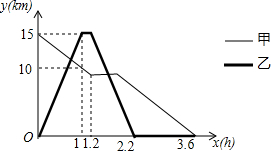 某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30℃ | B. | -16℃ | C. | -22℃ | D. | -18℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
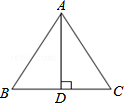 如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )
如图,已知等腰△ABC中,AB=AC,AD⊥BC,下列不正确的是( )| A. | BD=CD | B. | ∠DAB=∠DAC | ||
| C. | 当∠B=60°时,AB=2BD | D. | 高AD是△ABC的对称轴 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com