
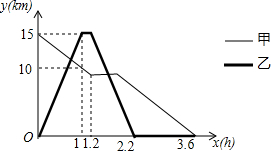
 某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.
某森林公园从正门到侧门有一条公路供游客运动,甲徒步从正门出发匀速走向侧门,出发一段时间开始休息,休息了0.6小时后仍按原速继续行走.乙与甲同时出发,骑自行车从侧门匀速前往正门,到达正门后休息0.2小时,然后按原路原速匀速返回侧门.图中折线分别表示甲、乙到侧门的路程y(km)与甲出发时间x(h)之间的函数关系图象.根据图象信息解答下列问题.分析 (1)根据函数图象可知点(0,15)和点(1,10)在甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数图象上,从而可以解答本题;
(2)根据函数图象可以分别求得甲乙刚开始两端对应的函数解析式,联立方程组即可求得第一次相遇的时间;
(3)根据函数图象可以得到在最后一段甲对应的函数解析式,乙到侧门时时间为2.2h,从而可以得到乙回到侧门时,甲到侧门的路程.
解答 解:(1)设甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=kx+b,
∵点(0,15)和点(1,10)在此函数的图象上,
∴$\left\{\begin{array}{l}{15=b}\\{10=k+b}\end{array}\right.$,
解得k=-5,b=15.
∴y=-5x+15.
即甲在休息前到侧门的路程y(km)与出发时间x(h)之间的函数关系式为:y=-5x+15.
(2)设乙骑自行车从侧门匀速前往正门对应的函数关系式y=kx,
将(1,15)代入可得k=15,
∴乙骑自行车从侧门匀速前往正门对应的函数关系式y=15x,
∴$\left\{\begin{array}{l}{y=-5x+15}\\{y=15x}\end{array}\right.$
解得x=0.75.
即第一次相遇时间为0.75h.
(3)乙回到侧门时,甲到侧门的路程是7km.
设甲休息了0.6小时后仍按原速继续行走对应的函数解析式为:y=kx+b.
将x=1.2代入y=-5x+15得,y=9.
∵点(1.8,9),(3.6,0)在y=kx+b上,
∴$\left\{\begin{array}{l}{1.8k+b=9}\\{3.6k+b=0}\end{array}\right.$,
解得k=-5,b=18.
∴y=-5x+18.
将x=2.2代入y=-5x+18,得y=7.
即乙回到侧门时,甲到侧门的路程是7km.
点评 本题考查一次函数的应用,解题的关键是能看懂题意,根据数形结合的数学思想,找出所求问题需要的条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 调查某食品添加剂是否超标宜用普查 | |
| B. | 甲、乙两组的平均成绩相同,方差分别是S甲2=3.6,S乙2=3.0,则两组成绩一样稳定 | |
| C. | 同一年出生的367名学生中,至少有两人的生日是同一天是随机事件 | |
| D. | 调查10名运动员兴奋剂的使用情况适宜全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
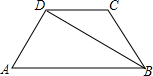 如图,在等腰梯形ABCD中,AB∥CD,AD=BC=3cm,∠A=60°,BD平分∠ABC,则梯形的周长( )cm.
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=3cm,∠A=60°,BD平分∠ABC,则梯形的周长( )cm.| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com