
【题目】已知如图所示,在平面直角坐标系中,四边形ABCO为梯形,BC∥AO,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,0).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒.
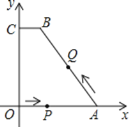
(1)求过A,B,C三点的抛物线的解析式;
(2)当t为何值时,PB与AQ互相平分;
(3)连接PQ,设△PAQ的面积为S,探索S与t的函数关系式.求t为何值时,S有最大值?最大值是多少?
【答案】(1)![]() ;(2)t=3;(3)当t=2时,S△PAQ有最大值为
;(2)t=3;(3)当t=2时,S△PAQ有最大值为![]() .
.
【解析】
(1)设出抛物线的解析式,运用待定系数法可以直接求出抛物线的解析式.
(2)根据PB与AQ互相平分可以得出四边形BQPA是平行四边形,得出QB=PA建立等量关系可以求出t值.
(3)是一道分段函数,分为Q点在AB上和在BC上根据三角形的面积公式表示出S于t的关系式就可以求出其答案.
解:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),代入A、B、C三点,得
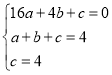
解得: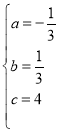
∴![]() .
.
(2)∵使得PB与AQ互相平分,
∴四边形BQPA是平行四边形,
∴BQ=PA,
∵AB=![]() =5,
=5,
∴2t-5=4-t,
解得:t=3.
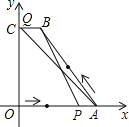
(3)由已知得AB=5,CB=1.
①当![]() 时,点Q在线段AB上运动,
时,点Q在线段AB上运动,
设P(xP,0),Q(xQ,yQ),∠OAB=θ,sinθ=![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当t=2时,S△PAQ有最大值为![]() .
.
②当![]() 时,点Q在线段BC上运动,则
时,点Q在线段BC上运动,则![]()
∴当![]() 时,S△PAQ有最大值为3.
时,S△PAQ有最大值为3.
∴综上所述,当t=2时,S△PAQ有最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕![]() ,且
,且![]() ,那么该矩形的周长为______cm.
,那么该矩形的周长为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
15 | 12 | 0 | 20 | 15 | 10 | 14 |
8 | 12 | 19 | 10 | 9 | 11 | 8 |
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.
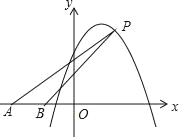
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地 2016年为做好“精准扶贫”,投入资金20万元用于异地安置,并规划投入资金逐年增加 .2018 年在 2016 年的基础上增加了8.8万元.
(1)从2016年到2018年,该地投入异地安置资金的年平均增长率为多少?
(2)若投入资金的年增长率继续保持不变,预计2019年将投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.

(1)根据图象,求当x≥3时的函数关系式;
(2)某人乘坐2.5km,应付多少钱?
(3)某人乘坐13km,应付多少钱?
(4)若某人付车费30.8元,出租车行驶了多少路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,DG交BC的,延长线于G,∠CFE=∠AEB
(1)若∠B=87°,求∠DCG的度数;
(2)AD与BC是什么位置关系?并说明理由;
(3)若∠DAB=α,∠DGC=β,直接写出α、β满足什么数量关系时,AE∥DG.
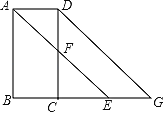
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)。
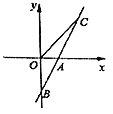
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△AOC =2,求点C的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图像.
(注:小明和妈妈始终在同一条笔直的公路上行走,图像上A、C、D三点在一条直线上)
(1)求线段BC的函数表达式;
(2)求点D坐标;
(3)当 x的值为 时,小明与妈妈相距1 500米.
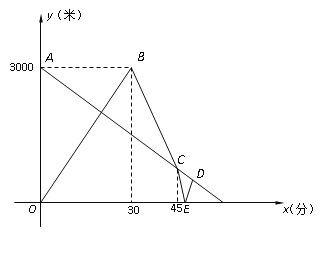
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com