
【题目】下表是小明某一周的收支情况,规定收入为正,支出为负.(单位:元)
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
15 | 12 | 0 | 20 | 15 | 10 | 14 |
8 | 12 | 19 | 10 | 9 | 11 | 8 |
(1)小明哪天的收入小于支出?答:
(2)小明这一周的平均支出是多少?
(3)小明这一周共有多少节余?
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.因为M是线段AB的中点,所以AM=MB=![]() AB
AB
B.在线段AM延长线上取一点B,如果AB=2AM,那么点M是线段AB的中点
C.因为A,M,B在同一直线上,且AM=MB,所以M是线段AB的中点
D.因为AM=MB,所以点M是AB的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
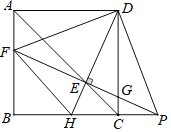
【题目】如图,正方形ABCD中,点H是边BC上一点(不与点B、点C重合).连接DH交正方形对角线AC于点E,过点E作DH的垂线交线段AB、CD于点F、G.延长FG与BC的延长线交于点P,连接DF、DP、FH.
(1)∠FDH=______°;DF与DP的位置关系是______,DF与DP的大小关系是______;
(2)在(1)的结论下,若AD=4,求△BFH的周长;
(3)在(1)的结论下,若BP=8,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淘宝11.11购物节期间,小垣妈妈在网上某品牌服装店按标价八折拍到一件学生外套,用支付宝支付了120元.爱思考的小垣进行了下列研究:
(1)该学生外套在网上的标价是 元.
(2)妈妈告诉小垣她在网上买到的学生外套商家可以获得20%的利润.根据妈妈的说法,一件学生外套的进价是多少元?
(3)小垣搜索发现标价相同的同款学生外套在网上另一店铺打折优惠,并规定订单金额满200元,可以使用30元店铺优惠券.她告诉妈妈如果一次购买2件只需要支付225元,那么该网店同款学生外套打几折进行优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一条长度为 a 的线段.
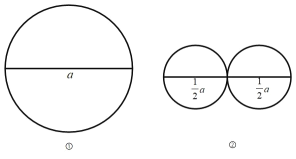
(1)如图①,以该线段为直径画一个圆,该圆的周长 C1 = ;如图②,分别以该线段的一半为直 径画两个圆,这两个圆的周长的和 C2 = (都用含 a 的代数式表示,结果保留 )
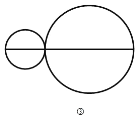
(2)如图③,在该线段上任取一点,再分别以两条小线段为直径画两个圆,这两个圆的周长的和为 C3 ,探索 C1 和 C3 的数量关系,并说明理由。
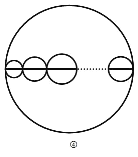
(3)如图④,当 a =10 时,以该线段为直径画一个大圆,再在大圆内画若干个小圆,这些小圆的直径都和 大圆的直径在同一条直线上,且小圆的直径的和等于大圆的直径,那么图中所有圆的周长的和为 (结 果保留 )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图所示,在平面直角坐标系中,四边形ABCO为梯形,BC∥AO,四个顶点坐标分别为A(4,0),B(1,4),C(0,4),O(0,0).一动点P从O出发以每秒1个单位长度的速度沿OA的方向向A运动;同时,动点Q从A出发,以每秒2个单位长度的速度沿A→B→C的方向向C运动.两个动点若其中一个到达终点,另一个也随之停止.设其运动时间为t秒.
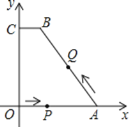
(1)求过A,B,C三点的抛物线的解析式;
(2)当t为何值时,PB与AQ互相平分;
(3)连接PQ,设△PAQ的面积为S,探索S与t的函数关系式.求t为何值时,S有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.
(1)公司在组装A、B两种型号的健身器材时,共有多少种组装方案?
(2)组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com