
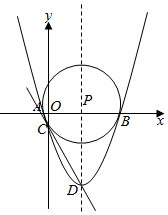
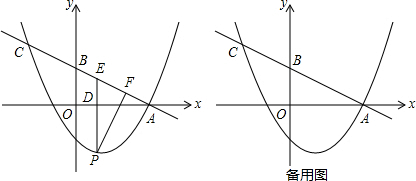
 如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).
如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$). 分析 利用抛物线与坐标的交点问题求出A、B、C点的坐标,再把抛物线解析式配成顶点式得到抛物线的对称轴方程和D点坐标,则可利用待定系数法求出CD的解析式,过P点作PH⊥直线CD于H,连结PB,CD交x轴于E点,抛物线的对称轴交x轴于F点,如图,易得F和E点坐标,设P(4,t),于是根据切线性质得到PH=PB,然后证明Rt△DPH∽Rt△DEF,通过相似比建立t的方程,再方程求出t即可得到P点坐标.
解答 解:当y=0时,$\frac{1}{3}$x2-$\frac{8}{3}$x-3=0,解得x1=-1,x2=9,则A(-1,0),B(9,0),
当x=0时,y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3=-3,则C(0,-3),
∵y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3=$\frac{1}{3}$(x-4)2-$\frac{25}{3}$,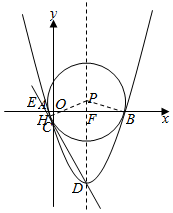
∴抛物线的对称轴为直线x=4,D点坐标为(4,-$\frac{25}{3}$),
设直线CD的解析式为y=kx+b,
把C(0,-3),D(4,-$\frac{25}{3}$)代入得$\left\{\begin{array}{l}{b=-3}\\{4k+b=-\frac{25}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-3}\end{array}\right.$,
∴直线CD的解析式为y=-$\frac{4}{3}$x-3,
过P点作PH⊥直线CD于H,连结PB,CD交x轴于E点,抛物线的对称轴交x轴于F点,如图,则F(4,0),E(-$\frac{9}{4}$,0),
∴EF=4-(-$\frac{9}{4}$)=$\frac{25}{4}$,FB=$\frac{25}{3}$,
∴DE=$\sqrt{F{D}^{2}+E{F}^{2}}$=$\frac{125}{12}$,
设P(4,t),则PD=t+$\frac{25}{3}$,PB=$\sqrt{(4-9)^{2}+{t}^{2}}$=$\sqrt{25+{t}^{2}}$,
∵以P为圆心的圆经过A,B两点,并且和直线CD相切,
∴PH=PB=$\sqrt{25+{t}^{2}}$,
∵∠PDH=∠EDF,
∴Rt△DPH∽Rt△DEF,
∴$\frac{PH}{EF}$=$\frac{PD}{ED}$,即$\frac{\sqrt{25+{t}^{2}}}{\frac{25}{4}}$=$\frac{t+\frac{25}{3}}{\frac{25}{12}}$,
整理得8t2-75t=0,解得t1=0,t2=$\frac{75}{8}$,
∴P点坐标为(4,0)或(4,$\frac{75}{8}$).
故答案为(4,0)或(4,$\frac{75}{8}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质和切线的性质;会求抛物线和一次函数图象与坐标轴的交点坐标;理解坐标与图形性质,记住两点间的距离公式;会应用相似比建立线段之间的关系.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
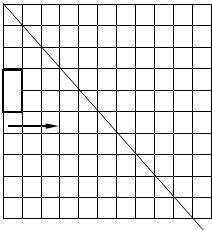 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.
如图,A,B两处是我国在南海上的两个观测站,从A处发现它的北偏西30°方向有一艘轮船,同时,从B处发现这艘轮船在它的北偏西60°方向.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
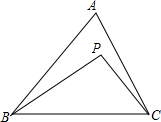 如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )
如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com