
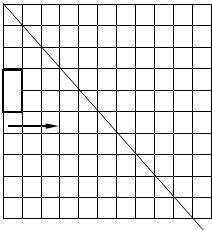
 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:解答题
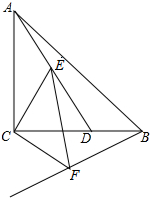 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
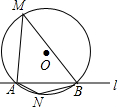 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
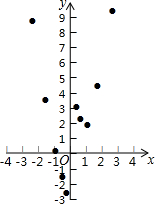 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | m | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
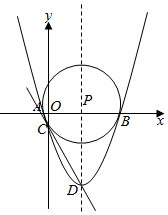 如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).
如图,已知二次函数y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3的图象与x轴交于A,B两点(点A在点B的左侧),与y轴的负半轴交于点C,顶点为D,作直线CD,点P是抛物线对称轴上的一点,若以P为圆心的圆经过A,B两点,并且和直线CD相切,则点P的坐标为(4,0)或(4,$\frac{75}{8}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com