
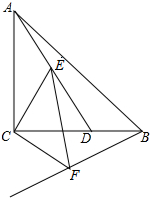
 如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.
如图,△ABC是等腰直角三角形,∠ACB=90°,AC=BC,D在BC上且∠BAD=15°,E是AD上的一点,现以CE为直角边,C为直角顶点在CE的下方作等腰直角三角形ECF,连接BF.分析 (1)注意到三角形CFB与三角形CEA全等,从而∠FBC=∠CAE,由条件可知∠CAE=30°,则∠ABF显然为定值;
(2)由于题目并没说G点在F点的左侧还是右侧,因此有两种情况.由于∠CBF=30°,故作CM垂直BF于M,则CM、BM可求,CG已知,由勾股定理可求出MG,从而可轻松算出答案.
解答 解:不变,∠ABF=75°.
证明:如图1,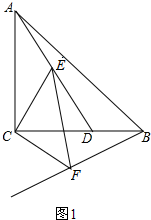
∵∠ACB=∠ECF=90°,
∴∠ACE=∠BCF,
∵AC=CB,CE=CF,
∴△ACE≌BCF,
∴∠CAE=∠CBF,
∵∠BAD=15°,∠CAB=∠ABC=45°,
∴∠CBF=∠CAE=30°,
∴∠ABF=∠ABC+∠CBF=75°.
(2)作CM⊥BF,垂足为M,如图2,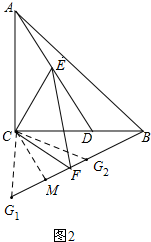
∵AB=6$\sqrt{2}$,
∴BC=AC=6,
∴CM=4,BM=4$\sqrt{3}$,
∵CG1=5,
∴MG1=4,
∴BG1=4+4$\sqrt{3}$,
同理可得:BG2=4$\sqrt{3}$-4.
点评 本题主要考查了全等三角形的判定与性质、等腰直角三角形的性质及其应用、勾股定理的应用、含特殊角的直角三角形的性质,难度中等.在求解线段长度时,“将特殊角放入直角三角形中”是基本原则,要引起重视,另外,注意本题第(2)问有两种情况,不要漏解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
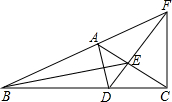 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
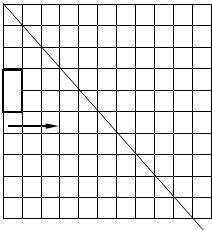 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
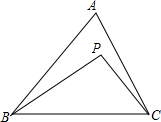 如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )
如图,点P是△ABC内的一点,有下列结论:①∠BPC>∠A;②∠BPC一定是钝角;③∠BPC=∠A+∠ABP+∠ACP.其中正确的结论为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com