
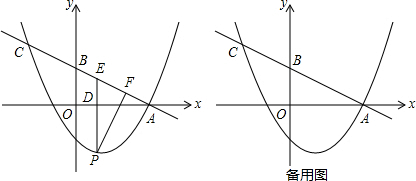
���� ��1��ֻ�������A��C�����꣬Ȼ�����ô���ϵ�����Ϳ���������ߵĽ���ʽ��ֻ�����OA��OB��AB��Ȼ���������Ǻ����Ķ���Ϳ����cos��BAO��ֵ��
��2�������D������Ϊ��m��0�����Ӷ������EP��AE����m�Ĵ���ʽ��ʾ������֤��PFE�ס�ADE��ֻ���������������ε����ʾͿɽ�����⣻
��3�����A1������Ϊ��p��q����������ת�����ʿɵõ�D1��p��q+5������E1��p+$\frac{5}{2}$��q+5������Ȼ��A1��D1������ͬʱ���������ϣ�ֻ���D1��E1���������Ϻ�A1��E1��������������������ۣ��Ϳɽ�����⣮
��� �⣺��1���ߵ�A����B�ֱ���ֱ��y=-$\frac{1}{2}$x+3��x�ԡ�y��Ľ��㣬
���A��������6��0������B��������0��3����
�ߵ�C��ֱ��y=-$\frac{1}{2}$x+3�ϣ���C�ĺ�����Ϊ-4��
���C��������-4��5����
�ߵ�A����C��������y=$\frac{1}{4}$x2+bx+c�ϣ�
��$\left\{\begin{array}{l}{9+6b+c=0}\\{4-4b+c=5}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-1}\\{c=-3}\end{array}\right.$��
����κ����Ľ���ʽΪy=$\frac{1}{4}$x2-x-3��
��Rt��AOB��
��A��6��0����B��0��3����
��OA=6��OB=3��
��AB=3$\sqrt{5}$��cos��BAO=$\frac{OA}{AB}$=$\frac{6}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{5}$��
��2�����D��������m��0��������
AD=6-m��P��m��$\frac{1}{4}$m2-m-3����E��m��-$\frac{1}{2}$m+3����
��PE=��-$\frac{1}{2}$m+3��-��$\frac{1}{4}$m2-m-3��=-$\frac{1}{4}$m2+$\frac{1}{2}$m+6��
AE=$\frac{AD}{cos��BAO}$=$\frac{\sqrt{5}}{2}$��6-m����
�ߡ�PFE=��ADE=90�㣬��PEF=��AED��
���PFE�ס�ADE��
��$\frac{{C}_{��PFE}}{{C}_{��ADE}}$=$\frac{PE}{AE}$����
��$\frac{\sqrt{5}}{2}$=$\frac{-\frac{1}{4}{m}^{2}+\frac{1}{2}m+6}{\frac{\sqrt{5}}{2}��6-m��}$��
�����ɵ�m2-7m+6=0��
���m1=1��m2=6����ȥ����
��D��1��0����E��1��$\frac{5}{2}$��
��AD=5��DE=$\frac{5}{2}$��AE=$\frac{5\sqrt{5}}{2}$��
��C��ADE=$\frac{15+5\sqrt{5}}{2}$��
��C��PEF=$\frac{\sqrt{5}}{2}$C��ADE=$\frac{15\sqrt{5}+25}{4}$��
��3�����A1��������p��q����
�ߡ�A1D1E1���ɡ�ADE��ƽ����һ��M��˳ʱ�뷽����ת90�����ã�
��D1E1��y�ᣬA1D1��x�ᣬD1E1=DE=$\frac{5}{2}$��A1D1=AD=5��
���D1��������p��q+5������E1��������p+$\frac{5}{2}$��q+5����
�ٵ�D1��E1����������ʱ��
D1��E1���ڶԳ���x=-$\frac{-1}{2��\frac{1}{4}}$=2�Գƣ�
����2-p=p+$\frac{5}{2}$-2��
���p=$\frac{3}{4}$��
��q+5=$\frac{1}{4}$p2-p-3=-$\frac{231}{64}$��
��q=-$\frac{551}{64}$��
���A1��������$\frac{3}{4}$��-$\frac{551}{64}$����
�ڵ�A1��E1����������ʱ��
����$\left\{\begin{array}{l}{q=\frac{1}{4}{p}^{2}-p-3}\\{q+5=\frac{1}{4}��p+\frac{5}{2}��^{2}-��p+\frac{5}{2}��-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{p=\frac{19}{4}}\\{q=-\frac{135}{64}}\end{array}\right.$��
���A1��������$\frac{19}{4}$��-$\frac{135}{64}$����
������������A1��������$\frac{3}{4}$��-$\frac{551}{64}$����$\frac{19}{4}$��-$\frac{135}{64}$����
���� ������Ҫ���������ô���ϵ��������κ����Ľ���ʽ���������ϵ������������ֱ���ϵ���������������������ε��ж������ʡ���һԪ���η��̡��ⷽ���顢���Ǻ����Ķ��塢���ɶ�����֪ʶ�����������������ܳ��ȵ������Ʊ��ǽ���ڣ�2��С��Ĺؼ���������ת�����ʵõ�A1��D1��E1����֮��Ĺ�ϵ���ǽ���ڣ�3��С��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
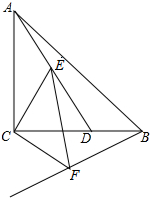 ��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AC=BC��D��BC���ҡ�BAD=15�㣬E��AD�ϵ�һ�㣬����CEΪֱ�DZߣ�CΪֱ�Ƕ�����CE���·�������ֱ��������ECF������BF��
��ͼ����ABC�ǵ���ֱ�������Σ���ACB=90�㣬AC=BC��D��BC���ҡ�BAD=15�㣬E��AD�ϵ�һ�㣬����CEΪֱ�DZߣ�CΪֱ�Ƕ�����CE���·�������ֱ��������ECF������BF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�D��BC��һ�㣬��AB=BD=3CD����cos��DAC=$\frac{7}{8}$��AD=6����AC=8��
��ͼ���ڡ�ABC�У�D��BC��һ�㣬��AB=BD=3CD����cos��DAC=$\frac{7}{8}$��AD=6����AC=8���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
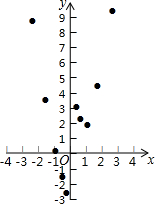 ����ѧϰ�����ľ��飬С���Ժ���y=x2+$\frac{1}{x}$��ͼ�������ʽ�����̽����������С����̽�����̣��벹����ɣ�
����ѧϰ�����ľ��飬С���Ժ���y=x2+$\frac{1}{x}$��ͼ�������ʽ�����̽����������С����̽�����̣��벹����ɣ�| ��x | �� | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | �� |
| ��y | �� | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | ��m | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
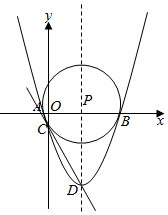 ��ͼ����֪���κ���y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C������ΪD����ֱ��CD����P�������߶Գ����ϵ�һ�㣬����PΪԲ�ĵ�Բ����A��B���㣬���Һ�ֱ��CD���У����P������Ϊ��4��0����4��$\frac{75}{8}$����
��ͼ����֪���κ���y=$\frac{1}{3}$x2-$\frac{8}{3}$x-3��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C������ΪD����ֱ��CD����P�������߶Գ����ϵ�һ�㣬����PΪԲ�ĵ�Բ����A��B���㣬���Һ�ֱ��CD���У����P������Ϊ��4��0����4��$\frac{75}{8}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
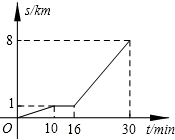 �ɶ��ж���·�ܻ��߿��ٹ����ѿ�ͨ��С��ӼҲ��е�������վ̨���ȹ�����ȥѧУ��ͼ�е����߱�ʾС����г�s ��ǧ�ף�������ʱ��t �����ӣ�֮��ĺ�����ϵ������˵��������ǣ�������
�ɶ��ж���·�ܻ��߿��ٹ����ѿ�ͨ��С��ӼҲ��е�������վ̨���ȹ�����ȥѧУ��ͼ�е����߱�ʾС����г�s ��ǧ�ף�������ʱ��t �����ӣ�֮��ĺ�����ϵ������˵��������ǣ�������| A�� | �����8ǧ�ף�������30���� | B�� | ���ȹ�����ʱ��Ϊ6���� | ||
| C�� | �����е��ٶ���100��/���� | D�� | ���������ٶ���350��/���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com