
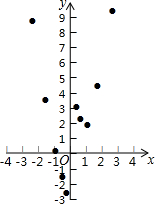 根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
根据学习函数的经验,小明对函数y=x2+$\frac{1}{x}$的图象与性质进行了探究.下面是小明的探究过程,请补充完成:| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{26}{3}$ | $\frac{7}{2}$ | 0 | -$\frac{7}{4}$ | -$\frac{26}{9}$ | $\frac{28}{9}$ | $\frac{9}{4}$ | 2 | $\frac{9}{2}$ | m | … |
分析 (1)根据分母不能为零即可写出x的取值范围.
(2)x=3代入解析式计算即可求出m.
(3)描点法画图即可.
(4)根据图象写一条符合该函数图象的性质即可.
解答 解;(1)函数y=x2+$\frac{1}{x}$的自变量x的取值范围是x≠0.
故答案为x≠0;
(2)x=3时,m=32+$\frac{1}{3}$=$\frac{28}{3}$.
故答案为$\frac{28}{3}$;
(3)该函数图象如图所示,
(4)该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开.
故答案为:该函数没有最大值或该函数没有最小值或该函数不经过第四象限或该函数在x=0处断开.
点评 本题考查函数的图象的性质,会用描点法画出函数图象,利用数形结合的思想写出函数的性质,是一条开放性题目,难度不大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
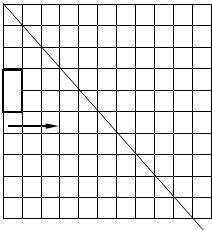 如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线
如图,矩形ABCD是一颗水平向右匀速飞行的“卫星”,直线l1是一束高能射线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
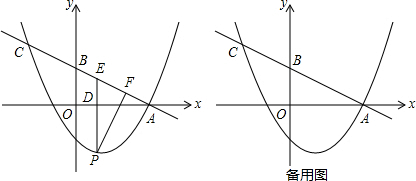
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com