
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
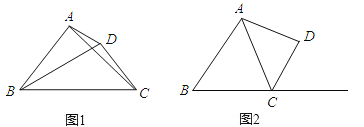
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
【答案】(1)④;(2)见解析;(3)存在这样一点E,使得四边形ABED为邻对等四边形,DE=![]()
【解析】
(1)根据中点四边形的特征,结合邻对等四边形的定义求解即可;
(2)延长CD至E,使CE=BA,根据“SAS”可证△ABC≌△ECB,从而BE=CA,∠BAC=∠E.利用等量代换可证BD=BE,从而∠BDE=∠E,然后可证明结论成立;
(3)在BC延长线上取一点E,使得CE=4,连接DE,四边形ABED即为邻对等四边形.连接AE,BD,由等腰三角形的性质和三角形外角的性质可证∠ABC=∠DEB,∠ACE=∠BCD.通过证明CE≌△BCD,可证BD=AE,从而四边形ABED为邻对等四边形.通过证明△ABC∽△DEC,利用相似三角形的性质可求出DE的长.
(1)①顺次连接任意四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
②顺次连接平行四边形各边中点所得的四边形是平行四边形,平行四边形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
③顺次连接矩形各边中点所得的四边形是菱形,菱形不具备一组邻角相等且对角线相等,故不是邻对等四边形;
④顺次连接菱形各边中点所得的四边形是矩形,矩形具备一组邻角相等且对角线相等,故是邻对等四边形;
故答案为④;
(2)∵AB>CD,故可延长CD至E,使CE=BA,
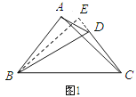
在△ABC与△ECB中,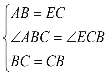 ,
,
∴△ABC≌△ECB.
∴BE=CA,∠BAC=∠E.
∵AC=DB,
∴BD=BE.
∴∠BDE=∠E.
∴∠CDB+∠BDE=∠CDB+∠E=∠BAC+∠CDB=180°.
即∠BAC与∠CDB互补.
(3)存在这样一点E,使得四边形ABED为邻对等四边形,
如图2,在BC延长线上取一点E,使得CE=4,
连接DE,四边形ABED即为邻对等四边形.
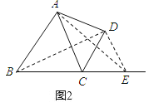
理由如下:
连接AE,BD,
∵CE=CD,
∴∠CDE=∠CED.
∵∠BCD=2∠B,
∴∠ABC=∠DEB,∠ACE=∠BCD.
在△ACE与△BCD中,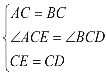 ,
,
∴△ACE≌△BCD.
∴BD=AE,四边形ABED为邻对等四边形.
∵∠CBA=∠CAB=∠CDE=∠CED,
∴△ABC∽△DEC.
∴![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
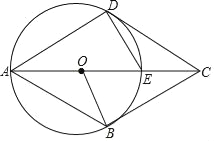
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
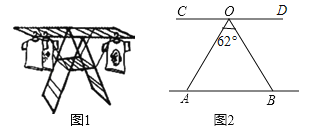
【题目】小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图,A,B两点立于地面,将晒衣架稳固张开,测得张角∠AOB=62°,立杆OA=OB=140cm,小梅的连衣裙穿在衣架后的总长度为122cm,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,等腰Rt△OAB的一条直角边OA 在x轴的正半轴上,点B在双曲线![]() 上,且∠BAO=90°,
上,且∠BAO=90°,![]() .
.
(1)求k的值及点A的坐标;
(2)△OAB沿直线OB平移,当点A恰好在双曲线上时,求平移后点A的对应点A′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=
的图象于点B.给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④CA=![]() AP.其中所有正确结论的序号是( )
AP.其中所有正确结论的序号是( )
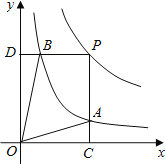
A. ①②③ B. ②③④ C. ①③④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
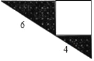
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时,点P的坐标为( )
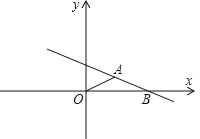
A. (1,1) B. (![]() ,3) C. (3,
,3) C. (3,![]() ) D. (2,2)
) D. (2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=2![]() ,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
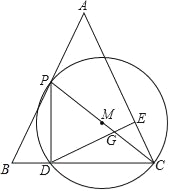
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com