
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
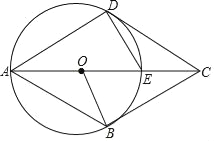
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
(1)先判断出∠2+∠3=90°,再判断出∠1=∠2即可得出结论;
(2)根据等腰三角形的性质得到∠3=∠COD=∠DEO=60°,根据平行线的性质得到∠4=∠1,根据全等三角形的性质得到∠CBO=∠CDO=90°,于是得到结论;
(3)先判断出△ABO≌△CDE得出AB=CD,即可判断出四边形ABCD是平行四边形,最后判断出CD=AD即可.
(1)如图,连接OD,
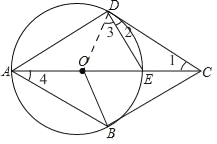
∵CD是⊙O的切线,
∴OD⊥CD,
∴∠2+∠3=∠1+∠COD=90°,
∵DE=EC,
∴∠1=∠2,
∴∠3=∠COD,
∴DE=OE;
(2)∵OD=OE,
∴OD=DE=OE,
∴∠3=∠COD=∠DEO=60°,
∴∠2=∠1=30°,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴∠BOC=∠DOC=60°,
在△CDO与△CBO中,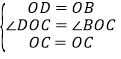 ,
,
∴△CDO≌△CBO(SAS),
∴∠CBO=∠CDO=90°,
∴OB⊥BC,
∴BC是⊙O的切线;
(3)∵OA=OB=OE,OE=DE=EC,
∴OA=OB=DE=EC,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴△ABO≌△CDE(AAS),
∴AB=CD,
∴四边形ABCD是平行四边形,
∴∠DAE=![]() ∠DOE=30°,
∠DOE=30°,
∴∠1=∠DAE,
∴CD=AD,
∴ABCD是菱形.


科目:初中数学 来源: 题型:
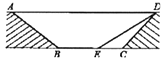
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3 000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价 (单位:元) | 可供出售的槟榔芋重量 (单位:千克) | |
现在出售 | 3 000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29 000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,航拍无人机从A处测得一幢建筑物顶部B处的仰角为45°、底部C处的俯角为65°,此时航拍无人机A处与该建筑物的水平距离AD为80米.求该建筑物的高度BC(精确到1米).(参考数据:sin65°=0.91,cos65°=0.42,tan65°=2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+3与y轴交于点A,与反比例函数y=![]() (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )

A. y=![]() B. y=-
B. y=-![]() C. y=
C. y=![]() D. y=-
D. y=-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB是⊙O的直径,![]() ,连接AC.
,连接AC.
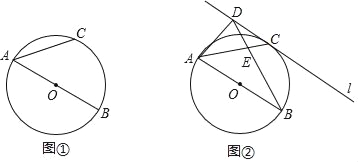
(1)求证:∠CAB=45°;
(2)如图②,直线l经过点C,在直线l上取一点D,使BD=AB,BD与AC相交于点E,连接AD,且AD=AE.
①求证:直线l是⊙O的切线;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
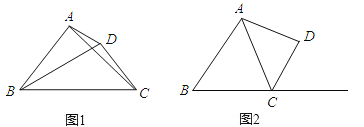
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com