
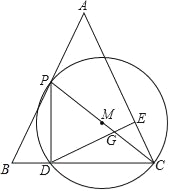
【题目】在△ABC中,AB=AC=2![]() ,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
【答案】![]()
【解析】
作AH⊥BC于H.首先证明△PDB∽△DEC∽△CEG∽△AHB,设BD=a,则有PD=PG=2a,CD=4-a,EC=![]() ,CG=
,CG=![]() ,推出PC=PG+CG=
,推出PC=PG+CG=![]() ,在Rt△PCD中,根据PD2+CD2=PC2,构建方程即可解决问题.
,在Rt△PCD中,根据PD2+CD2=PC2,构建方程即可解决问题.
如图,作AH⊥BC于H,
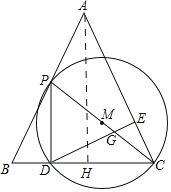
∵AB=AC=2![]() ,AH⊥BC,
,AH⊥BC,
∴∠B=∠ACD,BH=CH=2,AH=![]() =4,
=4,
∵PC是直径,
∴∠PDC=90°,
∵DE⊥AC,
∴∠CDP=∠CED=90°,
∵PD=PG,
∴∠PDG=∠PGD=∠CGE,
∵∠PDG+∠CDE=90°,∠CDE+∠ECD=90°,
∴∠PDG=∠ECD=∠B=∠EGC,
∵∠PDB=∠DEC=∠AHB=90°,
∴△PDB∽△DEC∽△CEG∽△AHB,设BD=a,
则有PD=PG=2a,CD=4-a,EC=![]() ,CG=
,CG=![]() ,
,
∴PC=PG+CG=![]() ,
,
在Rt△PCD中,∵PD2+CD2=PC2,
∴4a2+(4-a)2=(![]() )2,
)2,
解得a=![]() 或4(舍弃),
或4(舍弃),
∴BD=![]() .
.
故答案为:![]() .
.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
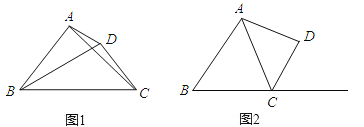
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
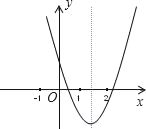
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P.若AB=6,BC=3![]() ,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=
,则下列结论:①F是CD的中点;②⊙O的半径是2;③AE=![]() CE;④S阴影=
CE;④S阴影=![]() .其中正确的个数为( )
.其中正确的个数为( )
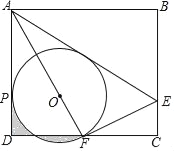
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用![]() 万元
万元![]() 与年产量
与年产量![]() 万件
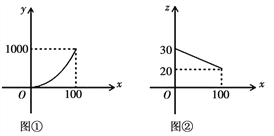
万件![]() 之间的函数图象是顶点为原点的抛物线的一部分
之间的函数图象是顶点为原点的抛物线的一部分![]() 如图
如图![]() 所示
所示![]() ;该产品的销售单价
;该产品的销售单价![]() 元
元![]() 件
件![]() 与年销售量
与年销售量![]() 万件
万件![]() 之间的函数图象是如图
之间的函数图象是如图![]() 所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元
所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元![]() 毛利润
毛利润![]() 销售额
销售额![]() 生产费用
生产费用![]()
![]() 请写出y与x以及z与x之间的函数关系式;
请写出y与x以及z与x之间的函数关系式;
![]() 求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
求w与x之间的函数关系式;并求年产量多少万件时,所获毛利润最大?最大毛利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
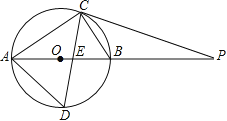
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°,开通隧道后,汽车从A地到B地大约可以少走多少千米(结果精确到1千米)?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
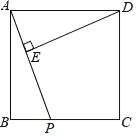
【题目】如图,在正方形ABCD中,AB=4,P是BC边上一动点(不与B,C重合),DE⊥AP于E.
(1)试说明△ADE∽△PAB;
(2)若PA=x,DE=y,请写出y与x之间的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com