
【题目】如图,⊙O的直径AB为10cm,弦BC为5cm,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE.
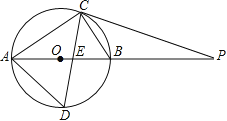
(1)求AC、AD的长;
(2)试判断直线PC与⊙O的位置关系,并说明理由.
【答案】(1)AC=8,AD=5![]() cm;(2)直线PC与⊙O相切,理由见解析.
cm;(2)直线PC与⊙O相切,理由见解析.
【解析】试题分析:(1)、连接BD,根据AB为直径,则∠ACB=∠ADB=90°,根据Rt△ABC的勾股定理求出AC的长度,根据CD平分∠ACB得出Rt△ABD是等腰直角三角形,从而得出AD的长度;(2)、连接OC,根据OA=OC得出∠CAO=∠OCA,根据PC=PE得出∠PCE=∠PEC,然后结合CD平分∠ACB得出∠ACE=∠ECB,从而得出∠PCB=∠ACO,根据∠ACB=90°得出∠OCP=90°,从而说明切线.
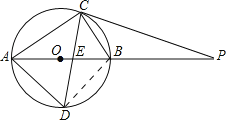
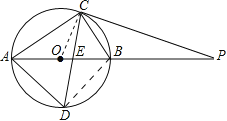
试题解析:(1)、①如图,连接BD, ∵AB是直径, ∴∠ACB=∠ADB=90°,
在RT△ABC中,AC=![]() =
=![]() =8cm,
=8cm,
②∵CD平分∠ACB, ∴AD=BD,∴Rt△ABD是直角等腰三角形, ∴AD=![]() AB=
AB=![]() ×10=5
×10=5![]() cm;
cm;
(2)、直线PC与⊙O相切,
理由:连接OC, ∵OC=OA,∴∠CAO=∠OCA, ∵PC=PE, ∴∠PCE=∠PEC,
∵∠PEC=∠CAE+∠ACE, ∵CD平分∠ACB, ∴∠ACE=∠ECB,∴∠PCB=∠ACO,∵∠ACB=90°,
∴∠OCP=∠OCB+∠PCB=∠ACO+∠OCB=∠ACB=90°, OC⊥PC,
∴直线PC与⊙O相切.


科目:初中数学 来源: 题型:
【题目】如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为( )平方米.
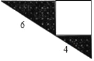
A. 3![]() B. 9 C. 12 D. 24
B. 9 C. 12 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
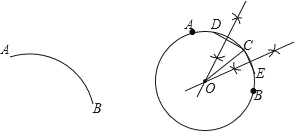
【题目】下面是“作出弧AB所在的圆”的尺规作图过程.
已知:弧AB.
求作:弧AB所在的圆.
作法:如图,
(1)在弧AB上任取三个点D,C,E;
(2)连接DC,EC;
(3)分别作DC和EC的垂直平分线,两垂直平分线的交点为点O.
(4)以 O为圆心,OC长为半径作圆,所以⊙O即为所求作的弧AB所在的圆.
请回答:该尺规作图的依据是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
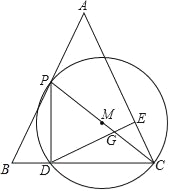
【题目】在△ABC中,AB=AC=2![]() ,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
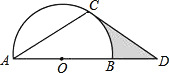
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ;cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ;tan(α+β)=![]() (1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=
(1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=![]() =1,利用上述公式计算下列三角函数①sin105°=
=1,利用上述公式计算下列三角函数①sin105°=![]() ,②tan105°=﹣2﹣
,②tan105°=﹣2﹣![]() ,③sin15°=
,③sin15°=![]() ,④cos90°=0,其中正确的个数有( )
,④cos90°=0,其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
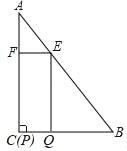
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
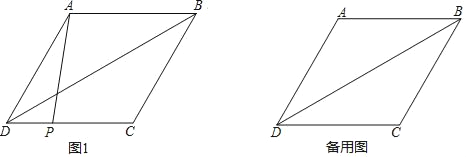
【题目】在菱形ABCD中,∠ADC=60°,BD是一条对角线,点P在边CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,在BD上取一点H,使HQ=HD,连接HQ,AH,PH.
(1)依题意补全图1;
(2)判断AH与PH的数量关系及∠AHP的度数,并加以证明;
(3)若∠AHQ=141°,菱形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知近视眼镜的度数y(度)与镜片焦距x(米)之间成如图所示的反比例函数关系,则眼镜度数y与镜片焦距x之间的函数解析式为( )

A. y=200x B. y=![]() C. y=100x D. y=
C. y=100x D. y=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com