
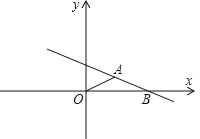
【题目】如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时,点P的坐标为( )
A. (1,1) B. (![]() ,3) C. (3,
,3) C. (3,![]() ) D. (2,2)
) D. (2,2)
科目:初中数学 来源: 题型:
【题目】如图①,AB是⊙O的直径,![]() ,连接AC.
,连接AC.
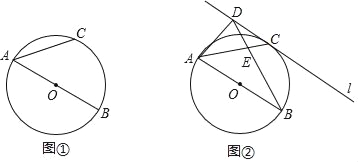
(1)求证:∠CAB=45°;
(2)如图②,直线l经过点C,在直线l上取一点D,使BD=AB,BD与AC相交于点E,连接AD,且AD=AE.
①求证:直线l是⊙O的切线;
②求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:有一组邻角相等且对角线相等的凸四边形叫做“邻对等四边形”.
概念理解
(1)下列四边形中属于邻对等四边形的有 (只填序号);
①顺次连接任意四边形各边中点所得的四边形;
②顺次连接平行四边形各边中点所得的四边形;
③顺次连接矩形各边中点所得的四边形;
④顺次连接菱形各边中点所得的四边形;
性质探究
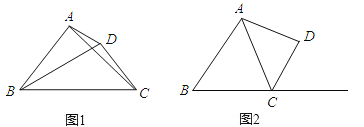
(2)如图1,在邻对等四边形ABCD中,∠ABC=∠DCB,AC=DB,AB>CD,求证:∠BAC与∠CDB互补;
拓展应用
(3)如图2,在四边形ABCD中,∠BCD=2∠B,AC=BC=5,AB=6,CD=4.在BC的延长线上是否存在一点E,使得四边形ABED为邻对等四边形?如果存在,求出DE的长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;
(2)求小丽投放的两袋垃圾不同类的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便孩子入学,小王家购买了一套学区房,交首付款15万元,剩余部分向银行贷款,贷款及贷款利息按月分期还款,每月还款数相同.计划每月还款y万元,x个月还清贷款,若y是x的反比例函数,其图象如图所示:
(1)求y与x的函数解析式;
(2)若小王家计划180个月(15年)还清贷款,则每月应还款多少万元?

查看答案和解析>>
科目:初中数学 来源: 题型:
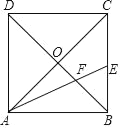
【题目】如图,正方形ABCD的边长为![]() +1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
+1,对角线AC、BD相交于点O,AE平分∠BAC分别交BC、BD于E、F,
(1)求证:△ABF∽△ACE;
(2)求tan∠BAE的值;
(3)在线段AC上找一点P,使得PE+PF最小,求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,在下列代数式中(1)a+b+c>0;(2)﹣4a<b<﹣2a(3)abc>0;(4)5a﹣b+2c<0; 其中正确的个数为( )
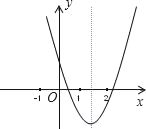
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°,开通隧道后,汽车从A地到B地大约可以少走多少千米(结果精确到1千米)?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com