
【题目】在Rt△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转一定的角度α得到△DEC,点A,B的对应点分别是D,E.

(1)当点E恰好在AC上时,如图①所示,求∠ADE的度数;
(2)若α=60°时,F是边AC的中点,如图②所示,求证:四边形BEDF是平行四边形.
【答案】(1)15°;(2)证明见解析.
【解析】
(1)如图①,利用旋转的性质得CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°,再根据等腰三角形的性质和三角形内角和计算出∠CAD,从而利用互余和计算出∠ADE的度数;
(2)如图②,利用直角三角形斜边上的中线性质得到BF=![]() AC,利用含30度的直角三角形三边的关系得到AB=
AC,利用含30度的直角三角形三边的关系得到AB=![]() AC,则BF=AB,再根据旋转的性质得到∠BCE=∠ACD=60°,CB=CE,DE=AB,从而得到DE=BF,△ACD和△BCE为等边三角形,接着证明△CFD≌△ABC得到DF=BC,然后根据平行四边形的判定方法得到结论.
AC,则BF=AB,再根据旋转的性质得到∠BCE=∠ACD=60°,CB=CE,DE=AB,从而得到DE=BF,△ACD和△BCE为等边三角形,接着证明△CFD≌△ABC得到DF=BC,然后根据平行四边形的判定方法得到结论.
解:(1)∵△ABC绕点C顺时针旋转α得到△DEC,点E恰好在AC上,
∴CA=CD,∠ECD=∠BCA=30°,∠DEC=∠ABC=90°.
∴∠CAD=∠CDA=![]() ×(180°﹣30°)=75°
×(180°﹣30°)=75°
∴∠ADE=90°﹣75°=15°.
(2)∵F是边A C的中点,
∴BF=![]() AC.
AC.
∵∠ACB=30°,
∴AB=![]() AC.
AC.
∴BF=AB.
∴△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°, BC=EC,DE=AB,AC=DC.
∴DE=BF,△ACD,△BCE是等边三角形.
∴BE=BC.
∴F是边AC的中点,
∴DF⊥AC,CF=BF=AB.
∴∠CFD=90°.
∴Rt△CFD≌Rt△ABC.
∴DF=BC.
∴DF=BE.
又∵BF=DE,
∴四边形BEDF是平行四边形.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
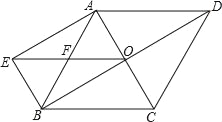
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
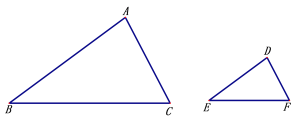
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
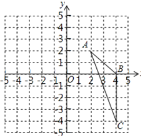
【题目】如图,在平面直角坐标系中,已知![]() 三个顶点的坐标分别是
三个顶点的坐标分别是![]() ,
,![]() ,
,![]() .
.
(1)请在图中画出![]() 向左平移6个单位长度后得到
向左平移6个单位长度后得到![]() ;
;
(2)以点O为位似中心,将![]() 缩小为原来的
缩小为原来的![]() ,得到
,得到![]() ,请在图中y轴右侧,画出
,请在图中y轴右侧,画出![]() ,并求出
,并求出![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连结BD,∠BAD=105°,∠DBC=75°.

(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与抛物线
与抛物线![]() :
:![]() 中,若
中,若![]() ,则称抛物线
,则称抛物线![]() ,
,![]() 为“窗帘”抛物线.
为“窗帘”抛物线.
(1)已知![]() 与
与![]() 是“窗帘”抛物线,
是“窗帘”抛物线,
①![]() 的值为______;
的值为______;
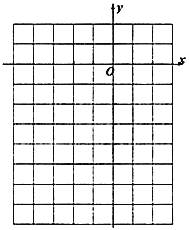
②在如图的坐标系中画出它们的大致图像,并直接写出它们的交点坐标.
(2)设抛物线![]() ,
,![]() ,
,![]()
![]() 的顶点分别为
的顶点分别为![]() ,
,![]() ,
,![]() ,
,
①判断它们是否是“窗帘”抛物线?答:______(填“是”或“不是”)
②若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)已知二次函数y=ax2+bx+c过点A(1,0),B(﹣3,0),C(0,﹣3)
(1)求此二次函数的解析式;
(2)在抛物线上存在一点P使△ABP的面积为6,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,直接写出抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,请用列表法或树状图法,求抽到的都是合格品的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com