
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
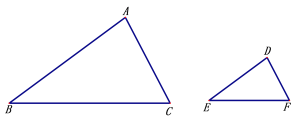
【答案】见解析
【解析】
(1)按照作一个角的平分线的作法作出一组对应角的平分线即可;
(2)首先根据相似三角形的对应角相等,由△ABC∽△DEF,得出∠A=∠D ,∠ABC =∠DEF ,再根据角平分线的定义,得出∠ABM=∠DEN,根据两角分别相等,两三角形相似,证明△ABM∽△DEN,继而得出对应边的比等于相似比.
(1)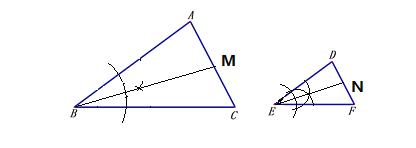
(2)如(1)图,已知△ABC∽△DEF,△ABC和△DEF的相似比为k,BM、EN分别是△ABC和△DEF的角平分线。求证:![]() =k.
=k.
证明:∵△ABC∽△DEF,,
∴∠A=∠D ,∠ABC =∠DEF ,,
∵BM、EN分别是△ABC和△DEF的角平分线,
∴∠ABM=![]() ∠ABC,∠DEN=
∠ABC,∠DEN=![]() ∠DEF,
∠DEF,
∴∠ABM=∠DEN,
∵∠A=∠D ,∠ABM=∠DEN,
∴△ABM∽△DEN,
∴![]() =k.
=k.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
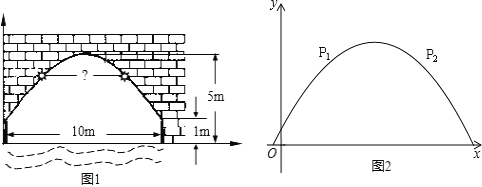
【题目】作为青岛市和李沧区的重点民生工程,经过8年不懈努力,李村河从一条城市臭水沟变成了一个美不胜收的湿地公园,因其卓越的治理效果,李村河上游综合治理工程荣获了住建部“中国人居环境范例奖”.下图是我区李村河上一座拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
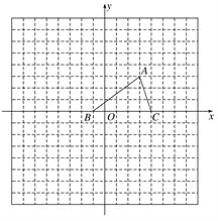
【题目】如图,已知△ABC的三个顶点的坐标分别为A(3,3)、B(-1,0)、C(4,0).
(1)经过平移,可使△ABC的顶点A与坐标原点O重合,请直接写出此时点C的对应点C1坐标;(不必画出平移后的三角形)
(2)将△ABC绕点B逆时针旋转90°,得到△A′BC′,画出△A′BC′并写出A′点的坐标;
(3)以点A为位似中心放大△ABC,得到△AB2C2,使放大前后的面积之比为1∶4,请你在网格内画出△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
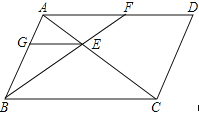
A. 4对B. 5对C. 6对D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
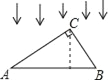
【题目】如图,在Rt△ABC中,∠C=90°,投影线方向如图所示,点C在斜边AB上的正投影为点D,
(1)试写出边AC、BC在AB上的投影;
(2)试探究线段AC、AB和AD之间的关系;
(3)线段BC、AB和BD之间也有类似的关系吗?请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
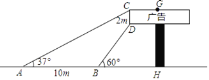
【题目】如图,长方形广告牌架在楼房顶部,已知CD=2m,经测量得到∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com