
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
【答案】(1)见解析;(2)①m=1;②PG的最小值=![]()
【解析】
(1)令y=0,再求出的方程的△是否大于等于0即可;
(2)①令y=0,解一元二次方程,再根据已知点A在点B的右侧,且![]() ,求解即可;②先假设与直线
,求解即可;②先假设与直线![]() 平行的直线l的关系式为
平行的直线l的关系式为![]() ,
,
若直线l与抛物线![]() 只有一个交点C,列方程,根据
只有一个交点C,列方程,根据![]() 得b的值,则点C到直线
得b的值,则点C到直线![]() 的距离就是PG的最小值.
的距离就是PG的最小值.
(1)当y=0时,![]()
![]() .
.
∴抛物线![]() 与x轴有交点;
与x轴有交点;
(2)①当y=0时,![]() ,
,
解得![]() 或
或![]() ,
,
∵点A在点B的右侧,
∴![]() ,
,
∵![]() ,
,
∴ 当![]() ,
,![]() 时,1+2
时,1+2![]() ,解得m=1,
,解得m=1,
此时![]() ,
,![]() ,满足
,满足![]() ,故m=1符合题意,
,故m=1符合题意,
当![]() ,
,![]() 时,
时,![]() ,解得m=2.
,解得m=2.
此时![]() ,
,![]() ,与
,与![]() 矛盾,故m=2不符合题意.
矛盾,故m=2不符合题意.
∴m=1;
②
当m=1时,抛物线解析式为![]() ,
,
∵点G![]() ,
,
∴点G在直线![]() 上.
上.
假设与直线![]() 平行的直线l的关系式
平行的直线l的关系式
为![]() ,
,
若直线l与抛物线![]() 只有一个交点C,
只有一个交点C,
则此时方程![]() 的
的![]() ,解得b=
,解得b=![]() .
.
∴直线l的关系式![]() ,
,
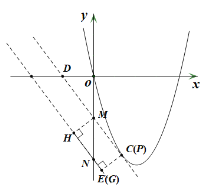
如图,直线l与x轴,y轴分别交于D,M两点,直线![]()
与y轴交于N点,
∴D(![]() ,0),M(0,
,0),M(0,![]() ).
).
∴OD=![]() ,OM=
,OM=![]() .
.
∴MN=![]() ,
,
DM=![]() =
=![]() ,
,
过点M作MH⊥HN,CE⊥EN,当P点与C点重合,G点与E点重合时,PG长最小,
此时△MHN∽△DOM,
∴![]() ,即
,即 ,
,
∴PG=MH=![]() ,
,
即PG的最小值是![]() .
.
故答案为:(1)见解析;(2)①m=1;②PG的最小值=![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】计数问题是我们经常遇到的一类问题,学会解决计数问题的方法,可以使我们方便快捷,准确无误的得到所要求的结果,下面让我们借助两个问题,了解计数问题中的两个基本原理---加法原理、乘法原理.
问题1.从青岛到大连可以乘坐飞机、火车、汽车、轮船直接到达.如果某一天中从青岛直接到达大连的飞机有3班,火车有4班,汽车有8班,轮船有5班,那么这一天中乘坐某种交通工具从青岛直接到达大连共有 种不同的走法:
问题2.从甲地到乙地有3条路,从乙地到丙地有4条路,那么从甲地经过乙地到丙地,共有 种不同的走法:
方法探究
加法原理:一般的,完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法。那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.
实践应用1
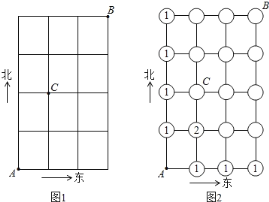
问题3.如图1,图中线段代表横向、纵向的街道,小明爸爸打算从A点出发开车到B点办事(规定必须向北走,或向东走,不走回头路),问他共有多少种不同的走法?其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,如果将走法数填入图2的空圆中,便可以借助所填数字回答:从A点出发到B点的走法共有 种:
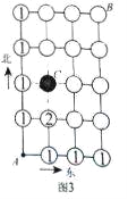
(2)根据上面的原理和图3的提示,请算出从A点出发到达B点,并禁止通过交叉点C的走法有 种.
(3)现由于交叉点C道路施工,禁止通行。小明爸爸如果任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是
实践应用2
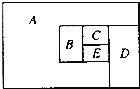
问题4.小明打算用 5种颜色给如下图的5个区域染色,每个区域染一种颜色,相邻的区域染不同的颜色,问共有 种不同的染色方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
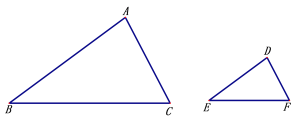
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:sinα=sin (180°-α),cosα=-cos (180°-α);若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点. ∠APC=∠CPB=60°.
(1)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
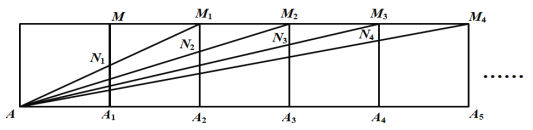
【题目】将2019个边长为1的正方形按如图所示的方式排列,点A,A1,A2,A3,……A2019和点M,M1,M2……,M2018是正方形的顶点,连接A1M,A2M1,A3M2,……A2018分别交正方形的边A1M,A2M1,A3M2,……A2018M2017于点N1,N2,N3……N2018,四边形M1N1A1A2的面积是![]() ,四边形M2N2A2A3的面积是
,四边形M2N2A2A3的面积是![]() ,…,则
,…,则![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
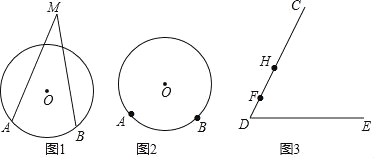
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com