
【题目】计数问题是我们经常遇到的一类问题,学会解决计数问题的方法,可以使我们方便快捷,准确无误的得到所要求的结果,下面让我们借助两个问题,了解计数问题中的两个基本原理---加法原理、乘法原理.
问题1.从青岛到大连可以乘坐飞机、火车、汽车、轮船直接到达.如果某一天中从青岛直接到达大连的飞机有3班,火车有4班,汽车有8班,轮船有5班,那么这一天中乘坐某种交通工具从青岛直接到达大连共有 种不同的走法:
问题2.从甲地到乙地有3条路,从乙地到丙地有4条路,那么从甲地经过乙地到丙地,共有 种不同的走法:
方法探究
加法原理:一般的,完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法。那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.
实践应用1
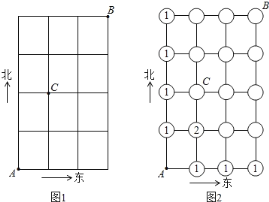
问题3.如图1,图中线段代表横向、纵向的街道,小明爸爸打算从A点出发开车到B点办事(规定必须向北走,或向东走,不走回头路),问他共有多少种不同的走法?其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,如果将走法数填入图2的空圆中,便可以借助所填数字回答:从A点出发到B点的走法共有 种:
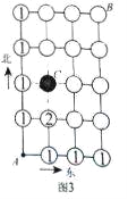
(2)根据上面的原理和图3的提示,请算出从A点出发到达B点,并禁止通过交叉点C的走法有 种.
(3)现由于交叉点C道路施工,禁止通行。小明爸爸如果任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是
实践应用2
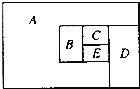
问题4.小明打算用 5种颜色给如下图的5个区域染色,每个区域染一种颜色,相邻的区域染不同的颜色,问共有 种不同的染色方法.
【答案】问题1:20;问题2:12;问题3:(1)35;(2)17;(3)![]() ;问题4:240种.
;问题4:240种.
【解析】
问题1. 根据一天中乘飞机有3种走法,乘火车有4种走法,乘汽车有8种走法,轮船有5种走法,再由加法原理求解即可,
问题2. 根据乘火车有3种走法,乘汽车有2种走法,再由乘法原理求解即可,
问题3.
(1)根据完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法.那么完成这件事共有N=m+n种不同的方法,则到达A点以外的任意交叉点的走法数只能是与其相邻的南边交叉点和西边交叉点的数字之和.从而计算出从A点到达其余各交叉点的走法数;
(2)此题有两种计算方法:方法一是先求从A点到B点,并经过交叉点C的走法数,再用从A点到B点总走法数减去它;方法二是删除与C点紧相连的线段,运用分类加法计数原理,算出从A点到B点并禁止通过交叉点C的走法;
(3)结合(1)和(2)的结论,即可求得概率.
问题4. 因为A与其它4个区域都相邻,所以先填A区域,有5种选择;那么B区域,有4种选择;由于C区域与A和B都相邻,所以有3种选择;同理,E区域与A、B、C都相邻,所以有2种选择;而D区域只与A、C、E相邻,不与B相邻,因此可以和B区域同色,所以D区域有2种选择;根据乘法原理可得共有:5×4×3×2×2=240(种)染色方法.
问题1. 一天中乘飞机有3种走法,乘火车有4种走法,乘汽车有8种走法,轮船有5种走法,每一种走法都可以从青岛直接到达大连,按加法原理,所以共有3+4+8+5=20种不同的走法.
问题2. 因为乘火车有3种走法,乘汽车有2种走法,所以乘一次火车再接乘一次汽车从甲地到乙地,按乘法原理,共有3×2=6种不同的走法.
问题3.
(1)∵完成从A点到B点必须向北走,或向东走,
∴到达A点以外的任意交叉点的走法数只能是与其相邻的南边交叉点和西边交叉点的数字之和,故使用分类加法计数原理,由此算出从A点到达其余各交叉点的走法数,填表如图1.
答:从A点到B点的走法共有35种.
(2)方法一:可先求从A点到B点,并经过交叉点C的走法数,再用从A点到B点总走法数减去它,即得从A点到B点,但不经过交叉点C的走法数.
完成从A点出发经C点到B点这件事可分两步,先从A点到C点,再从C点到B点,
使用分类加法计数原理,算出从A点到C点的走法是3种,见图2;算出从C点到B点的走法为6种,见图3,再运用分步乘法计数原理,得到从A点经C点到B点的走法有3×6=18种.
∴从A点到B点但不经过C点的走法数为35-18=17种.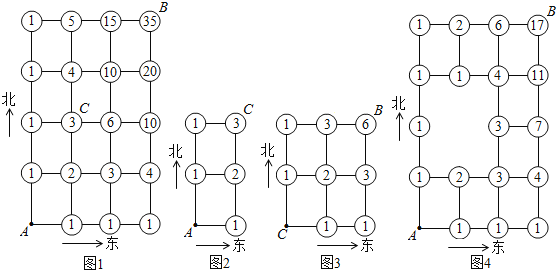
方法二:由于交叉点C道路施工,禁止通行,故视为相邻道路不通,可删除与C点紧相连的线段,运用分类加法计数原理,算出从A点到B点并禁止通过交叉点C的走法有17种.从A点到各交叉点的走法数见图4,
∴从A点到B点并禁止经过C点的走法数为35-18=17种.
(3)P(顺利开车到达B点)=![]() .
.
答:任选一种走法,顺利开车到达B点的概率是![]() .
.
问题4. 解:乘法原理可得:
5×4×3×2×2=240(种).
答:共有240种染色方法.


科目:初中数学 来源: 题型:
【题目】下框中是小明对一道题目的解答以及老师的批改.
题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2∶1,在温室内,沿前侧内墙保留3 m的空地,其他三侧内墙各保留1 m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288 m2?

解:设矩形蔬菜种植区域的宽为x_m,则长为2xm,
根据题意,得x·2x=288.
解这个方程,得x1=-12(不合题意,舍去),x2=12,
所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)
答:当温室的长为28 m,宽为14 m时,矩形蔬菜种植区域的面积是288 m2.
我的结果也正确!
小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.
结果为何正确呢?
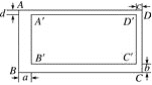
(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样?
(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD∶AB=2∶1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线和x轴交于两点A、B,和y轴交于点C,已知A、B两点的横坐标分别为﹣1,4,△ABC是直角三角形,∠ACB=90°,则此抛物线顶点的坐标为_____.
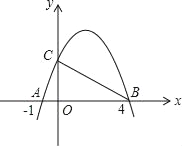
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为青岛市和李沧区的重点民生工程,经过8年不懈努力,李村河从一条城市臭水沟变成了一个美不胜收的湿地公园,因其卓越的治理效果,李村河上游综合治理工程荣获了住建部“中国人居环境范例奖”.下图是我区李村河上一座拱桥的截面图,拱桥桥洞上沿是抛物线形状.抛物线两端点与水面的距离都是1m,拱桥的跨度为10cm.桥洞与水面的最大距离是5m.桥洞两侧壁上各有一盏距离水面4m的景观灯.现把拱桥的截面图放在平面直角坐标系中.
(1)求抛物线的解析式;
(2)求两盏景观灯之间的水平距离.
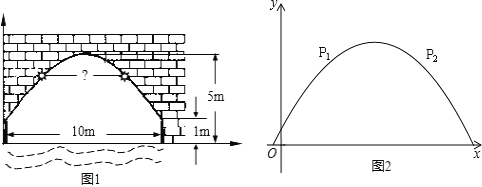
查看答案和解析>>
科目:初中数学 来源: 题型:
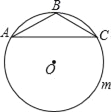
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在第一象限内作射线![]() ,与
,与![]() 轴的夹角为
轴的夹角为![]() ,在射线
,在射线![]() 上取点
上取点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .在抛物线
.在抛物线![]() 上取点
上取点![]() ,在
,在![]() 轴上取点
轴上取点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点,且以点
为顶点,且以点![]() 为直角顶点的三角形与
为直角顶点的三角形与![]() 全等,则符合条件的点
全等,则符合条件的点![]() 的坐标是________.
的坐标是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com