
【题目】如图,在第一象限内作射线![]() ,与
,与![]() 轴的夹角为
轴的夹角为![]() ,在射线
,在射线![]() 上取点
上取点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .在抛物线
.在抛物线![]() 上取点
上取点![]() ,在
,在![]() 轴上取点
轴上取点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点,且以点
为顶点,且以点![]() 为直角顶点的三角形与
为直角顶点的三角形与![]() 全等,则符合条件的点
全等,则符合条件的点![]() 的坐标是________.
的坐标是________.

【答案】![]() ,
,![]()
【解析】
由于AH的长度没有确定,所以只要以点Q为直角顶点的三角形与△AOH相似,那么两者就有可能全等;当点Q为直角顶点时,若∠POQ=30°或∠POQ=60°时,都符合解题要求,那么可根据∠POx的度数求出直线OP的解析式,然后联立抛物线的解析式即可得点P的坐标.
解:在Rt△AOH中,∠AOH=30°;
由题意,可知:当∠POQ=30°或∠POQ=60°时,以点Q为直角顶点的△POQ与△AOH全等,故∠POx=60°或∠POx=30°;
①当∠POx=60°时,kOP=tan60°=![]() ,所以,直线OP:y=
,所以,直线OP:y=![]() x,联立抛物线的解析式,
x,联立抛物线的解析式,![]() ,解得:
,解得:![]() 或
或![]()
即P![]() ,
,
②当∠POx=30°时,kOP=tan30°=![]() ,所以,直线OP:y=
,所以,直线OP:y=![]() x,联立抛物线的解析式,
x,联立抛物线的解析式, ,解得:
,解得:![]() 或
或
即P![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,线段OD=OC.
(1)求抛物线的解析式;
(2)抛物线上是否存在点M,使得⊿CDM是以CD为直角边的直角三角形?若存在,请求出M点的坐标;若不存在,请说明理由.
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,,连接QE.若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点的移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计数问题是我们经常遇到的一类问题,学会解决计数问题的方法,可以使我们方便快捷,准确无误的得到所要求的结果,下面让我们借助两个问题,了解计数问题中的两个基本原理---加法原理、乘法原理.
问题1.从青岛到大连可以乘坐飞机、火车、汽车、轮船直接到达.如果某一天中从青岛直接到达大连的飞机有3班,火车有4班,汽车有8班,轮船有5班,那么这一天中乘坐某种交通工具从青岛直接到达大连共有 种不同的走法:
问题2.从甲地到乙地有3条路,从乙地到丙地有4条路,那么从甲地经过乙地到丙地,共有 种不同的走法:
方法探究
加法原理:一般的,完成一件事有两类不同的方案,在第一类方案中有m种不同的方法,在第二类方案中有n种不同的方法。那么完成这件事共有N=m+n种不同的方法,这是分类加法计数原理;完成一件事需要两个步骤,做第一步有m种不同的方法,做第二步有n种不同的方法.那么完成这件事共有N=m×n种不同的方法,这就是分步乘法计数原理.
实践应用1
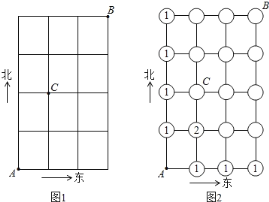
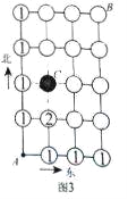
问题3.如图1,图中线段代表横向、纵向的街道,小明爸爸打算从A点出发开车到B点办事(规定必须向北走,或向东走,不走回头路),问他共有多少种不同的走法?其中从A点出发到某些交叉点的走法数已在图2填出.
(1)根据以上原理和图2的提示,算出从A出发到达其余交叉点的走法数,如果将走法数填入图2的空圆中,便可以借助所填数字回答:从A点出发到B点的走法共有 种:
(2)根据上面的原理和图3的提示,请算出从A点出发到达B点,并禁止通过交叉点C的走法有 种.
(3)现由于交叉点C道路施工,禁止通行。小明爸爸如果任选一种走法,从A点出发能顺利开车到达B点(无返回)概率是
实践应用2
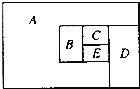
问题4.小明打算用 5种颜色给如下图的5个区域染色,每个区域染一种颜色,相邻的区域染不同的颜色,问共有 种不同的染色方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
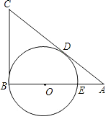
【题目】已知:如图,在![]() 中,
中,![]() 度.
度.![]() 是
是![]() 上一点,以
上一点,以![]() 为圆心、
为圆心、![]() 为半径的圆与
为半径的圆与![]() 交于点
交于点![]() ,与
,与![]() 切于点
切于点![]() ,
,![]() ,
,![]() .设
.设![]() 是线段
是线段![]() 上的动点(
上的动点(![]() 与
与![]() 、
、![]() 不重合),
不重合),![]() .
.
![]() 求
求![]() 的长;
的长;
![]() 求
求![]() 为何值时,以
为何值时,以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形;
为顶点的三角形是等腰三角形;
![]() 在点
在点![]() 的运动过程中,
的运动过程中,![]() 与
与![]() 的外接圆能否相切?若能,请证明;若不能,请说明理由;
的外接圆能否相切?若能,请证明;若不能,请说明理由;
![]() 请再提出一个与动点
请再提出一个与动点![]() 有关的数学问题,并直接写出答案.
有关的数学问题,并直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .则
.则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,线段
上的射影是________点,线段![]() 在
在![]() 上的射影是___,线段
上的射影是___,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
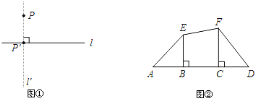
查看答案和解析>>
科目:初中数学 来源: 题型:
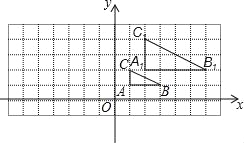
【题目】如图,在平面直角坐标系网格中,将△ABC进行位似变换得到△A1B1C1.
(1)△A1B1C1与△ABC的位似比是 ;
(2)画出△A1B1C1关于y轴对称的△A2B2C2;
(3)设点P(a,b)为△ABC内一点,则依上述两次变换后,点P在△A2B2C2内的对应点P2的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
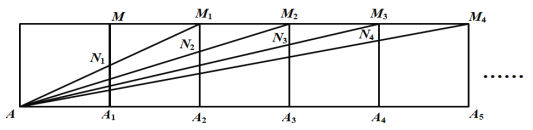
【题目】将2019个边长为1的正方形按如图所示的方式排列,点A,A1,A2,A3,……A2019和点M,M1,M2……,M2018是正方形的顶点,连接A1M,A2M1,A3M2,……A2018分别交正方形的边A1M,A2M1,A3M2,……A2018M2017于点N1,N2,N3……N2018,四边形M1N1A1A2的面积是![]() ,四边形M2N2A2A3的面积是
,四边形M2N2A2A3的面积是![]() ,…,则
,…,则![]() 为( )
为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com