
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )
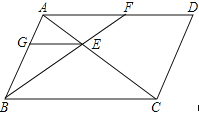
A. 4对B. 5对C. 6对D. 7对
【答案】B
【解析】
试题根据平行四边形的性质得出AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,推出△ABC≌△CDA,即可推出△ABC∽△CDA,根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
解:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
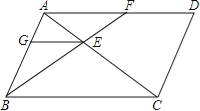
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∞△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,有长为24米的篱笆,围成中间隔有一道篱笆的长方形的花圃,且花圃的长可借一段墙体(墙体的最大可用长度a=10m),设AB的长为xm,所围的花圃面积为ym2,则y的最大值是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知平面内一点![]() 与一直线
与一直线![]() ,如果过点
,如果过点![]() 作直线
作直线![]() ,垂足为
,垂足为![]() ,那么垂足
,那么垂足![]() 叫做点
叫做点![]() 在直线
在直线![]() 上的射影;如果线段
上的射影;如果线段![]() 的两个端点
的两个端点![]() 和
和![]() 在直线
在直线![]() 上的射影分别为点
上的射影分别为点![]() 和
和![]() ,那么线段
,那么线段![]() 叫做线段
叫做线段![]() 在直线
在直线![]() 上的射影.
上的射影.
![]() 如图②,
如图②,![]() 、
、![]() 为线段
为线段![]() 外两点,
外两点,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() .则
.则![]() 点在
点在![]() 上的射影是________点,
上的射影是________点,![]() 点在
点在![]() 上的射影是________点,线段
上的射影是________点,线段![]() 在
在![]() 上的射影是___,线段
上的射影是___,线段![]() 在
在![]() 上的射影是________;
上的射影是________;
![]() 根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
根据射影的概念,说明:直角三角形斜边上的高是两条直角边在斜边上射影的比例中项.(要求:画出图形,写出说理过程.)
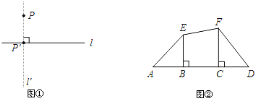
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.
(1)求证:EF=AE﹣BE;
(2)联结BF,如课![]() =
=![]() .求证:EF=EP.
.求证:EF=EP.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的中线,AE=EF=FC,下面给出三个关系式:①AD=2AG;②GE:BE=1:3;③![]() ,其中正确的是( )
,其中正确的是( )

A. ①② B. ①②③ C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
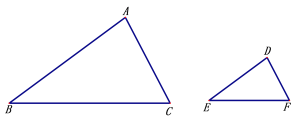
【题目】求证:相似三角形对应角的角平分线之比等于相似比.要求:
①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线,不写作法,保留作图痕迹;
②在完成作图的基础上,写出已知、求证,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点. ∠APC=∠CPB=60°.
(1)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与函数y=![]() (x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=
(x>0)的图象交于点A(m,2),B(2,n).过点A作AC平行于x轴交y轴于点C,在y轴负半轴上取一点D,使OD=![]() OC,且△ACD的面积是6,连接BC.
OC,且△ACD的面积是6,连接BC.
(1)求m,k,n的值;
(2)求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com