
【题目】在平面直角坐标系中,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() .
.
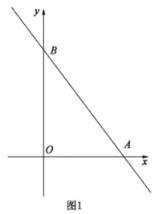

(1)如图1,求![]() 的值;
的值;
(2)如图2,经过点![]() 的直线
的直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,交
,交![]() 于点
于点![]() ,设线段
,设线段![]() 长为
长为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
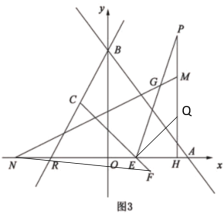
(3)如图3,在(2)的条件下,点![]() 在第四象限,
在第四象限,![]() 交
交![]() 于点
于点![]() ,
,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
, ![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,连接
,连接![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)先用b表示出点B和点A的坐标,然后利用勾股定理列出方程即可求出b的值;
(2)联立直线BC的解析式和直线AB的解析式即可用n表示出点C的坐标,从而求出点D的坐标,从而求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)过点C作CS⊥x轴于S,过点F作FT⊥x轴于T,过点G作GD⊥y轴于D,MN与y轴交于点I,根据相似三角形判定可得△RSC∽△ROB,列出比例式即可求出OR和CS,然后根据等角的锐角三角函数相等求出ON,再根据等腰直角三角形的性质求出NE,然后结合已知条件和等角的锐角三角函数相等求出TF,即可求出结论.
解:(1)当x=0时,y=b;当y=0时,x=![]()
∴点B的坐标为(0,b),点A的坐标为(![]() ,0)
,0)
∴OB=b,OA=![]()
根据勾股定理OB2+OA2=AB2
b 2+(![]() )2=102
)2=102
解得:b=8或-8(不符合已知条件,舍去)
∴b=8
(2)直线BC的解析式为![]() ,直线AB的解析式为
,直线AB的解析式为![]()
联立![]()
解得:![]()
∴点C的坐标为(-2,-2n)
∵![]()
∴点D的纵坐标为-2n
将y=-2n代入![]() 中,解得:x=
中,解得:x=![]()
∴点D的坐标为![]()
∴线段![]() 长
长![]() =
=![]() -(-2)=
-(-2)=![]()
(3)过点C作CS⊥x轴于S,过点F作FT⊥x轴于T,过点G作GD⊥y轴于D,MN与y轴交于点I
∴OD=![]() ,GD=
,GD=![]()

由(2)知点C坐标为(-2,-2n)
∴CS=-2n,OS=2
∵![]() ,CS∥y轴
,CS∥y轴
∴RB=2RC,△RSC∽△ROB
∴![]()
即![]()
解得:n=-2,OR=4
∴CS=4
∵![]() ,GD∥x轴
,GD∥x轴
∴![]() =∠DGI
=∠DGI
∴![]() =tan∠DGI
=tan∠DGI
∴![]()
即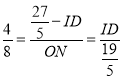
解得:![]()
∵![]()
∴∠CES=∠AEF=45°,∠QEH=∠QEF-∠AEF=45°
∴△CES、△EFT和△EHQ都是等腰直角三角形
∴CS=SE=4,ET=TF=![]() , EH=HQ,设EH=HQ=a,则EQ=
, EH=HQ,设EH=HQ=a,则EQ=![]()
∴EN=ON+OE=ON+SE-OS=9
∵![]() ,
,![]()
∴EF=![]() ,PM=a,PH=9,
,PM=a,PH=9,
∴NH=EN+EH=9+a,MH=PH-PM=9-a
∴![]() =
=![]()
∴![]()
解得:a=3
∴EF=![]()
∴TF=![]()
∴S△EFN=![]() EN·TF=
EN·TF=![]() ×9×1=
×9×1=![]()


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
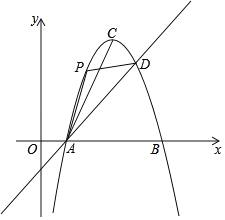
【题目】如图,直线y=x﹣1与抛物线y=﹣x2+6x﹣5相交于A、D两点.抛物线的顶点为C,连结AC.
(1)求A,D两点的坐标;
(2)点P为该抛物线上一动点(与点A、D不重合),连接PA、PD.
①当点P的横坐标为2时,求△PAD的面积;
②当∠PDA=∠CAD时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极创建全国文明城市,某市对某路口的行人交通违章情况进行了![]() 天的调查,将所得数据绘制成如下统计图(图2不完整):
天的调查,将所得数据绘制成如下统计图(图2不完整):
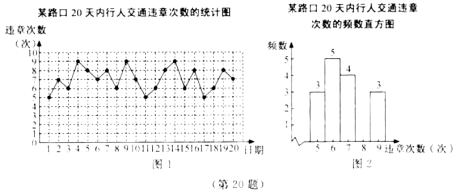
请根据所给信息,解答下列问题:
(1)第![]() 天,这一路口的行人交通违章次数是多少次?这
天,这一路口的行人交通违章次数是多少次?这![]() 天中,行人交通违章
天中,行人交通违章![]() 次的有多少天?
次的有多少天?
(2)请把图2中的频数直方图补充完整;(温馨提示:请画在答题卷相对应的图上)
(3)通过宣传教育后,行人的交通违章次数明显减少.经对这一路口的再次调查发现,平均每天的行人交通违章次数比第一次调查时减少了![]() 次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
次,求通过宣传教育后,这一路口平均每天还出现多少次行人的交通违章?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 的方格纸中,每个小正方形的边长均为1,线段
的方格纸中,每个小正方形的边长均为1,线段![]() 的端点
的端点![]() 、
、![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
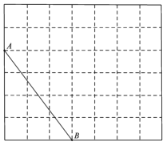
(1)在图中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点
,点![]() 在小正方形顶点上,且
在小正方形顶点上,且![]() ;
;
(2)在图中画出等腰三角形![]() ,点
,点![]() 在小正方形的顶点上,且
在小正方形的顶点上,且![]() 的面积为
的面积为![]() ;
;
(3)连接![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 两地相向而行,甲车从
两地相向而行,甲车从![]() 地出发
地出发![]() 后乙车从
后乙车从![]() 地出发,若甲车到达
地出发,若甲车到达![]() 地后直接按原路原速返回,而乙车到达
地后直接按原路原速返回,而乙车到达![]() 地后,先休息
地后,先休息![]() 再按原路原速返回.如图是甲、乙两车离
再按原路原速返回.如图是甲、乙两车离![]() 地距离
地距离![]() (单位:
(单位:![]() ),
),![]() (单位:
(单位:![]() )与甲车的行驶时间
)与甲车的行驶时间![]() (单位:
(单位:![]() )之间的函数图象.
)之间的函数图象.
(1)甲车的速度是 ![]() .乙车的速度是
.乙车的速度是 ![]() .点
.点![]() 的坐标是
的坐标是
(2)求线段![]() 和
和![]() 的函数关系式;
的函数关系式;
(3)甲、乙两车在行驶的过程中相遇了几次?直接写出当甲、乙两车相遇时甲车行驶的时间,并求出当两车最后一次相遇时,此时两车距![]() 地的距离
地的距离
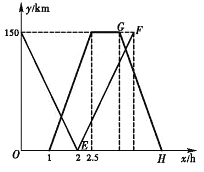
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,抛物线与
的左侧,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
(1)求抛物线的函数表达式;
(2)设![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为线段
为线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() 及抛物线于点
及抛物线于点![]() 、点
、点![]() ,当
,当![]() 是锐角三角形时,求
是锐角三角形时,求![]() 的取值范围.
的取值范围.
(3)在(2)的前提下,设![]() ,求
,求 ![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将:矩形纸片ABCD沿对角线AC剪开,得到△ABC和△ACD.并且量得AB=2cm,AC=4cm.
操作发现:
(1)将图1中的△ACD以点A为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的△
,得到如图2所示的△![]() ,过点C作
,过点C作![]() 的平行线,与
的平行线,与![]() 的延长线交于点E,则四边形
的延长线交于点E,则四边形![]() 的形状是 .
的形状是 .
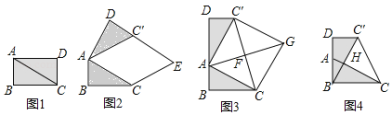
(2)创新小组将图1中的△ACD以点A为旋转中心,按逆时针方向旋转,使B、A、D三点在同一条直线上,得到如图3所示的△![]() ,连接
,连接![]() ,取
,取![]() 的中点F,连接AF并延长至点G,使FG=AF,连接CG、
的中点F,连接AF并延长至点G,使FG=AF,连接CG、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将△ABC沿着BD方向平移,使点B与点A重合,此时A点平移至![]() 点,
点,![]() 与
与![]() 相交于点H,如图4所示,连接
相交于点H,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B(﹣1,0)两点,与y轴交于点C,则下列四个结论:①ac<0;②2a+b=0;③﹣1<x<3时,y<0;④4a+c<0.其中所有正确结论的序号是( )
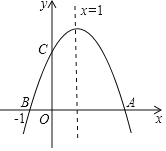
A.①②④B.①③④C.①②③D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com