
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,2).
相交于点A(m,2).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,且满足PA=OA. 直接写出点P的坐标.

【答案】(1)![]() ;(2)画图见解析;(3)P(0,4)或P(2,0).
;(2)画图见解析;(3)P(0,4)或P(2,0).
【解析】试题分析:
(1)把点A的坐标代入一次函数的解析式求出m的值,得到点A的坐标,再把所得点A的坐标代入反比例函数的解析式![]() 解得
解得![]() 的值,即可求得反比例函数的解析式;
的值,即可求得反比例函数的解析式;
(2)根据(1)中所得函数解析式,描点,连线,并利用反比例函数图象的两个分支关于原点对称即可画出两函数的图象了;
(3)先求出OA的长度,再分点P在x轴上和点P在y轴上两种情况分析解答即可.
试题解析:
(1)把点A(m,2)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,
,
∴点A的坐标为:(1,2),
把点A(1,2)代入![]() 得:
得: ![]() ,
,
∴反比例函数的解析式为: ![]() ;
;
(2)列表如下:
|
| 1 | 2 |
|
|
| 2 | 2 |
|
|
| 2 | 2 |
|
如图,在坐标系中描点,然后过两点画直线可得一次函数![]() 的图象,过两点画平滑的曲线可得反比例函数
的图象,过两点画平滑的曲线可得反比例函数![]() 在第一象限内的图象,再根据反比例函数图象的两个分支关于原点对称即可画出反比例函数
在第一象限内的图象,再根据反比例函数图象的两个分支关于原点对称即可画出反比例函数![]() 在第三象限内的图象.
在第三象限内的图象.

(3)如下图,∵点A的坐标为(1,2),
∴OA=![]() .
.
①当点P在y轴上时,可设其坐标为(0,y),
∵PA=OA,
∴![]() ,解得:
,解得: ![]() (与原点重合,舍去),
(与原点重合,舍去),
∴此时点P的坐标为(0,4);
②当点P在x轴上时,可设其坐标为(x,0),
∵PA=OA,
∴![]() ,解得:
,解得: ![]() (与点O重合,舍去),
(与点O重合,舍去),
∴点P的坐标为(2,0);
综上所述,点P的坐标为:P(0,4)或P(2,0).



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
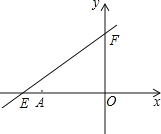
【题目】如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0)
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由;
,并说明理由;
(4)问在x轴上是否存在点Q,使得△EFQ为等腰三角形?若存在,求出符合条件的Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
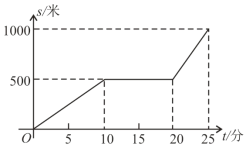
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;王老师吃早餐用了 分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
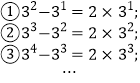
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,BD是一条对角线,∠DBC=30°,∠DBA=45°,∠C=70°.若DC=a,AB=b, 请写出求tan∠ADB的思路.(不用写出计算结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满了一定量的气体,当温度不变时,气球内气体的压强![]() (kPa)是气体体积
(kPa)是气体体积![]() (m3)的反比例函数,其图像如图所示.
(m3)的反比例函数,其图像如图所示.

(1)求这个反比例函数的表达式;
(2)当气球内的体积为气体1.6m3时,求气体压强![]() 的值:
的值:
(3)当气球内的气体压强大于150kPa时,气球将爆炸,为了安全起见,气体的体积不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com