
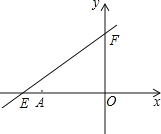
【题目】如图,直线y=kx+6与x轴、y轴分别交于点E,F,点E的坐标为(﹣8,0),点A的坐标为(﹣6,0)
(1)求k的值;
(2)若点P(x,y)是第二象限内的直线上的一个动点,在点P的运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,探究:当点P运动到什么位置时,△OPA的面积为![]() ,并说明理由;
,并说明理由;
(4)问在x轴上是否存在点Q,使得△EFQ为等腰三角形?若存在,求出符合条件的Q的坐标;若不存在,请说明理由.
【答案】(1)k=![]() ;(2)S=
;(2)S=![]() x+18(﹣8<x<0);(3)点P(﹣
x+18(﹣8<x<0);(3)点P(﹣![]() ,
,![]() )时,△OPA的面积为
)时,△OPA的面积为![]() ;(4)存在,符合条件的Q的坐标为(﹣18,0)或(2,0)或(8,0)或(﹣
;(4)存在,符合条件的Q的坐标为(﹣18,0)或(2,0)或(8,0)或(﹣![]() ,0)
,0)
【解析】
(1)将点E的坐标代入解析式中即可求出结论;
(2)由题意可得y=![]() x+6,然后求出点A的坐标,根据三角形的面积公式即可求出结论;
x+6,然后求出点A的坐标,根据三角形的面积公式即可求出结论;
(3)把S=![]() 代入S=
代入S=![]() x+18即可求出结论;
x+18即可求出结论;
(4)根据等腰三角形腰的情况分类讨论,画出对应的图形,然后根据等腰三角形的性质和勾股定理即可求出结论.
解:(1)∵直线y=kx+6经过点E(﹣8,0),
∴﹣8k+6=0,
解得k=![]() ;
;
(2)∵点P(x,y)是第二象限内的直线上的一个动点,
∴y=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6,
∴S=![]() OAy=
OAy=![]() ×6×(
×6×(![]() x+6)=
x+6)=![]() x+18.
x+18.
即S=![]() x+18(﹣8<x<0);
x+18(﹣8<x<0);
(3)把S=![]() 代入S=
代入S=![]() x+18
x+18
得![]() =
=![]() x+18,
x+18,
解得x=﹣![]() ,
,
∴当点P(﹣![]() ,
,![]() )时,△OPA的面积为
)时,△OPA的面积为![]() ;
;
(4)如图,∵E(﹣8,0),F(0,6)
∴OE=8,OF=6,EF=10,
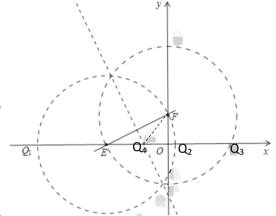
①以E为圆心以EF为半径作圆交x轴于Q1、Q2,
则Q1(﹣18,0),Q2(2,0),
②以F为圆心以EF为半径作圆交x轴于Q3,
易知FO垂直平分EQ3,
则Q3(8,0),
③作EF的垂直平分线交x轴于Q4,
∴Q4E= Q4F,设Q4O=x,则Q4E= Q4F=8-x,
由勾股定理可得![]()
即![]()
解得:x=![]()
∴Q4(﹣![]() ,0).
,0).
综上,符合条件的Q的坐标为(﹣18,0)或(2,0)或(8,0)或(﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )

A.2.2米B.2.3米C.2.4米D.2.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
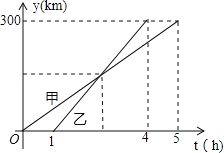
【题目】甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:①A,B两城相距300千米;②乙车比甲车晚出发1小时,却早到1小时; ③乙车出发后2小时追上甲车; ④当甲、乙两车相距50千米时,t=![]() 或
或![]() .其中正确的结论有_____.
.其中正确的结论有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
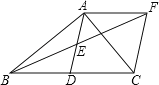
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:AD=AF;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.
(1)求甲、乙每天能生产多少万只口罩?
(2)问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】顶点都在格点上的三角形叫做格点三角形,如图,在4×4的方格纸中,△ABC是格点三角形.
(1)在图1中,以点C为对称中心,作出一个与△ABC成中心对称的格点三角形DEC,直接写出AB与DE的位置关系;
(2)在图2中,以AC所在的直线为对称轴,作出一个与△ABC成和对称的格点三角形AFC,直接写出△BCF是什么形状的特殊三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
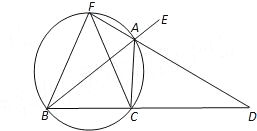
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点A(m,2).
相交于点A(m,2).
(1)求反比例函数的表达式;
(2)画出直线和双曲线的示意图;
(3)若P是坐标轴上一点,且满足PA=OA. 直接写出点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com